Miscellaneous (IB SL)

$\def\iixi#1#2{\left(\begin{array}{c}#1\\#2\end{array}\right)}\let\frac=\dfrac$

1

(IB/sl/2019/November/Paper2/q2) [Maximum mark: 5] Consider the lines $L_{1}$ and $L_{2}$ with respective equations $$L_{1}: y=-\frac{2}{3} x+9 \text { and } L_{2}: y=\frac{2}{5} x-\frac{19}{5} .$$ (a) Find the point of intersection of $L_{1}$ and $L_{2}$. [2] A third line, $L_{3}$, has gradient $-\frac{3}{4}$ (b) Write down a direction vector for $L_{3}$. [1] $L_{3}$ passes through the intersection of $L_{1}$ and $L_{2}$. (c) Write down a vector equation for $L_{3}$. [2]

2	(IB/sl/2016/November/Paper1/q7) [Maximum mark: 7] Let $f(x)=m-\frac{1}{x}$, for $x \neq 0 .$ The line $y=x-m$ intersects the graph of $f$ in two distinct points. Find the possible values of $m$.

3	(IB/sl/2015/May/paper2tz2/q7) [Maximum mark: 8] Let $f(x)=k x^{2}+k x$ and $g(x)=x-0.8$. The graphs of $f$ and $g$ intersect at two distinct points. Find the possible values of $k$.

4	(IB/sl/2019/May/paper1tz2/q6) [Maximum mark: 7] Solve $\log _{4}(2-x)=\log _{16}(13-4 x)$.

5	(IB/sl/2018/November/Paper1/q4) [Maximum mark: 6] Let $b=\log _{2} a$, where $a>0$. Write down each of the following expressions in terms of $b$. (a) $\log _{2} a^{3}$[2] (b) $\log _{2} 8 a$[2] (c) $\log _{k} a$[2]

6	(IB/sl/2018/May/paper1tz2/q7) [Maximum mark: 8] An arithmetic sequence has $u_{1}=\log _{c}(p)$ and $u_{2}=\log _{c}(p q)$, where $c>1$ and $p, q>0$. (a) Show that $d=\log _{\mathrm{c}}(g)$.[2] (b) Let $p=c^{2}$ and $q=c^{3}$. Find the value of $\sum_{n=1}^{20} n_{*}$.[6]

7	(IB/sl/2017/November/Paper1/q7) [Maximum mark: 7] Consider $f(x)=\log _{x}\left(6 x-3 x^{2}\right)$, for $0 < x < 2$, where $k>0$. The equation $f(x)=2$ has exactly one solution. Find the value of $k$.

8	(IB/sl/2017/May/paper1tz2/q7) [Maximum mark: 7] Solve $\log _{2}(2 \sin x)+\log _{2}(\cos x)=-1$, for $2 \pi < x < \frac{5 \pi}{2}$.

9	(IB/sl/2016/May/paper1tz2/q3) [Maximum mark: 6] Let $x=\ln 3$ and $y=\ln 5$. Write the following expressions in terms of $x$ and $y$. (a) $\ln \left(\frac{5}{3}\right)$. [2] (b) $\ln 45$. [4]

10	(IB/sl/2015/May/paper1tz1/q3) [Maximum mark: 6] (a) Given that $2^{\prime \prime}=8$ and $2^{n}=16$, write down the value of $m$ and of $n$. [2] (b) Hence or otherwise solve $8^{2 x+1}=16^{2 x-3}$. [4]

11

(IB/sl/2016/May/paper2tz1/q7) [Maximum mark: 8] Note: One decade is 10 years A population of rare birds, $P$, can be modelled by the equation $P_{0}=P_{3} \mathrm{e}^{\text {th }}$, where $P_{0}$ is the initial population, and $t$ is measured in decades. After one decade, it is estimated that $\frac{P_{1}}{P_{0}}=0.9$. (a) (i) Find the value of $k$. (ii) Interpret the meaning of the value of $k$. [3] (b) Find the least number of whole years for which $\frac{P_{t}}{P_{0}} < 0.75$. [5]

12

(IB/sl/2019/November/Paper1/q2) [Maximum mark: 6] In a class of 30 students, 18 are fluent in Spanish, 10 are fluent in French, and 5 are not fluent in either of these languages. The following venn diagram shows the events 'fluent in Spanish" and "fluent in French". The values $m, n, p$ and $q$ represent numbers of students. (a) Write down the value of $q$. [1] (b) Find the value of $n$. [2] (c) Write down the value of $m$ and of $p$. [3]

13

(IB/sl/2018/November/Paper2/q1) [Maximum mark: 6] In a group of 35 students, some take art class $(A)$ and some take music class $(M) .5$ of these students do not take either class. This information is shown in the following Venn diagram. (a) Write down the number of students in the group who take art class. [2] (b) One student from the group is chosen at random. Find the probability that (i) the student does not take art class: (ii) the student takes either art class or music class, but not both. [4]

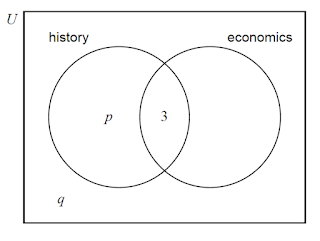
14

(IB/sl/2017/May/paper1tz1/q1) [Maximum mark: 6] In a group of 20 girls, 13 take history and 8 take economics. Three girls take both history and economics, as shown in the following venn diagram. The values $p$ and $q$ represent numbers of girls. (a) Find the value of (i) $p$; (ii) $q$. [4] (b) A girl is selected at random. Find the probability that she takes economics but not history. [2]

 

Answer

1](a) (12,1) (b) $\iixi{-4}{3}$ (c) $r=\iixi{12}{1} +t \iixi{-4}{3}$

2] $\quad m<-1$ or $m>1$

3] $k<0.2, k>5$

4] $ x=-3 $

5](a) $3 b$ (b) $3+b$ (c) $\frac{b}{3}$

6](a) show (b) 610

7] $k=\sqrt{3}$

8] $x=\frac{25 \pi}{12}, \frac{29 \pi}{12}$

9] (a) $y-x$ (b) $2 x+y$

10](a) $\quad m=3, n=4$ (b) $x=7.5$

11](a)(i) $\quad k=\ln 0.9$ (ii) population is decreasing (b) 28

12](a) 5 (b) 3 (c) 15,7

13](a) $17$ (b) (i) $\frac{18}{35}$ (ii) $\frac{24}{35}$

14](a)(i) $\quad p=10$ (ii) $q=2$ (b) $\frac{1}{4}$