CIE Surd (2020)

1

(CIE 0606/2018/w/13/q3) Do not use a calculator in this question. In this question, all lengths are in centimetres. A triangle $A B C$ is such that angle $B=90^{\circ}, A B=5 \sqrt{3}+5$ and $B C=5 \sqrt{3}-5$. (i) Find, in its simplest surd form, the length of $A C$. (ii) Find $\tan B C A$, giving your answer in the form $a+b \sqrt{3}$, where $a$ and $b$ are integers. [3]

2

(CIE 0606/2018/w/21/q3) Do not use a calculator in this question. (a) Simplify $(\sqrt{2}+2 \sqrt{5})(4 \sqrt{2}-3 \sqrt{5})$, giving your answer in the form $a+b \sqrt{c}$, where $a, b$ and $c$ are integers. (b) Simplify $\frac{4-3 \sqrt{6}}{\sqrt{3}+\sqrt{2}}$, giving your answer in the form $p \sqrt{3}+q \sqrt{2}$, where $p$ and $q$ are integers.

3	(CIE 0606/2018/w/22/q7) Solve the quadratic equation $(1-\sqrt{3}) x^{2}+x+(1+\sqrt{3})=0$, giving your answer in the form $a+b \sqrt{3}$, where $a$ and $b$ are constants.

4

(CIE 0606/2019/w/11/q8) Do not use a calculator in this question. In this question, all lengths are in centimetres.  The diagram shows the trapezium $A B C D$ in which angle $A D C$ is $90^{\circ}$ and $A B$ is parallel to $D C$. It is given that $A B=4+3 \sqrt{5}, \quad D C=11+2 \sqrt{5}$ and $A D=7+\sqrt{5}$. (i) Find the perimeter of the trapezium, giving your answer in simplest surd form. (ii) Find the area of the trapezium, giving your answer in simplest surd form.

5

(CIE 0606/2019/m/12/q7) Do not use a calculator in this question. All lengths in this question are in centimetres.  The diagram shows the trapezium $A B C D$, where $A B=2+3 \sqrt{5}, D C=6+3 \sqrt{5}, A D=10-2 \sqrt{5}$ and angle $A D C=90^{\circ}$. (i) Find the area of $A B C D$, giving your answer in the form $a+b \sqrt{5}$, where $a$ and $b$ are integers. (ii) Find $\cot B C D$, giving your answer in the form $c+d \sqrt{5}$, where $c$ and $d$ are fractions in their simplest form. [3]

6

(CIE 0606/2019/s/13/q7) Do not use a calculator in this question. In this question, all lengths are in centimetres.  The diagram shows the triangle $A B C$ such that $A B=2 \sqrt{5}-1, B C=2+\sqrt{5}$ and angle $A B C=90^{\circ}$. (i) Find the exact length of $A C$. (ii) Find $\tan A C B$, giving your answer in the form $p+q \sqrt{r}$, where $p, q$ and $r$ are integers. (iii) Hence find $\sec ^{2} A C B$, giving your answer in the form $s+t \sqrt{u}$ where $s, t$ and $u$ are integers. [2]

7	(CIE 0606/2019/s/21/q4) Without using a calculator, express $\frac{(\sqrt{5}-3)^{2}}{\sqrt{5}+1}$ in the form $p \sqrt{5}+q$, where $p$ and $q$ are integers.

8	(CIE $0606 / 2019 / \mathrm{w} / 22 / \mathrm{q} 11$ ) Do not use a calculator in this question. Solve the quadratic equation $(\sqrt{5}-3) x^{2}+3 x+(\sqrt{5}+3)=0$, giving your answers in the form $a+b \sqrt{5}$, where $a$ and $b$ are constants.

9	(CIE 0606/2019/w/23/q6) Do not use a calculator in this question. (i) Find $\tan ACB$ in the form $r+s\sqrt 3$, where $r$ and $s$ are integers. [3] (ii) Find $A C$ in the form $t \sqrt{u}$, where $t$ and $u$ are integers and $t \neq 1$. [3]

10	(CIE $0606 / 2020 / \mathrm{s} / 11 / \mathrm{q} 4$ ) DO NOT USE A CALCULATOR IN THIS QUESTION. Find the positive solution of the equation $(5+4 \sqrt{7}) x^{2}+(4-2 \sqrt{7}) x-1=0$, giving your answer in the form $a+b \sqrt{7}$, where $a$ and $b$ are fractions in their simplest form.

11

(CIE $0606 / 2020 / \mathrm{m} / 12 / \mathrm{q} 5$ ) DO NOT USE A CALCULATOR IN THIS QUESTION. In this question all lengths are in centimetres.  The diagram shows the isosceles triangle $A B C$, where $A B=A C$ and $B C=2+4 \sqrt{3}$. The height, $A D$, of the triangle is $5-\sqrt{3}$. (a) Find the area of the triangle $A B C$, giving your answer in the form $a+b \sqrt{3}$, where $a$ and $b$ are integers. (b) Find $\tan A B C$, giving your answer in the form $c+d \sqrt{3}$, where $c$ and $d$ are integers. (c) Find $\sec ^{2} A B C$, giving your answer in the form $e+f \sqrt{3}$, where $e$ and $f$ are integers.

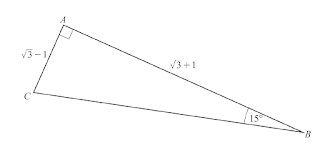
12

(CIE $0606 / 2020 / \mathrm{w} / 21 / \mathrm{q} 6)$ DO NOT USE A CALCULATOR IN THIS QUESTION. In this question all lengths are in centimetres.  In the diagram above $A C=\sqrt{3}-1, A B=\sqrt{3}+1$, angle $A B C=15^{\circ}$ and angle $C A B=90^{\circ}$. (a) Show that $\tan 15^{\circ}=2-\sqrt{3}$. (b) Find the exact length of $B C$.

13	(CIE 0606/2020/s/22/q2) DO NOT USE A CALCULATOR IN THIS QUESTION. The point $(1-\sqrt{5}, p)$ lies on the curve $y=\frac{10+2 \sqrt{5}}{x^{2}}$, Find the exact value of $p$, simplifying your answer.

14

$(\mathrm{CIE} 0606 / 2020 / \mathrm{w} / 22 / \mathrm{q} 8)$ DO NOT USE A CALCULATOR IN THIS QUESTION. In this question lengths are in centimetres.   (a) Given that the area of the triangle $A B C$ is $5.5 \mathrm{~cm}^{2}$, find the exact length of $A C$. Write your answer in the form $a+b \sqrt{3}$, where $a$ and $b$ are integers. (b) Show that $B C^{2}=c+d \sqrt{3}$, where $c$ and $d$ are integers to be found.

15	(CIE $0606 / 2020 / \mathrm{w} / 23 / \mathrm{q} 11)$ DO NOT USE A CALCULATOR IN THIS QUESTION. Solve the quadratic equation $(\sqrt{7}-2) x^{2}-4 x+(\sqrt{7}+2)=0$, giving each of your answers in the form $a+b \sqrt{7}$, where $a$ and $b$ are constants. [7]

16	(CIE 0606/2020/s/23/q5) DO NOT USE A CALCULATOR IN THIS QUESTION. (a) Simplify $\frac{\sqrt{128}}{\sqrt{72}}$ (b) Simplify $\frac{1}{1+\sqrt{3}}-\frac{\sqrt{3}}{3+2 \sqrt{3}}$, giving your answer as a fraction with an integer denominator. [4]

Answer 

1. (i) $A C=10 \sqrt{2}$

(ii) $\tan B C A=2+\sqrt{3}$

2. (a) $5 \sqrt{10}$

(b) $10 \sqrt{3}-13 \sqrt{2}$

3. $x=1+\sqrt{3}$ or $x=-\frac{1}{2}-\frac{\sqrt{3}}{2}$

4. (i) $P=22+6 \sqrt{5}+6 \sqrt{3}$

(ii) $A=65+25 \sqrt{5}$

5. (i) $10+22 \sqrt{5}$

(ii) $\frac{1}{2}+\frac{\sqrt{5}}{10}$

6. (i) $A C=\sqrt{30}$ (ii) $\tan A C B=12-5 \sqrt{5}$ (iii) $\sec ^{2} A C B=270-120 \sqrt{5}$

7. $6 \sqrt{5}-11$

8. $\quad x=3+\sqrt{5}, x=\frac{-(3+\sqrt{5})}{4}$

9. (i) $\tan A C B=2+\sqrt{3}$

(ii) $A C=2 \sqrt{6}$

10. $\quad x=\frac{6}{2 !}+\frac{1}{29} \sqrt{7}$

11. (a) $A=9 \sqrt{3}-1$

(b) $\sqrt{3}-1$

(c) $5-2 \sqrt{3}$

12. (a) proof

(b) $B C=2 \sqrt{2}$

13. $p=5+2 \sqrt{5}$

14. (a) $A C=4 \sqrt{3}-2$

(b) $B C^{2}=65-34 \sqrt{3}$

15. $x=2+\sqrt{7}, x=\frac{2}{3}+\frac{1}{3} \sqrt{7}$

16. (a) $\frac{4}{3}$

(b) $\frac{9 \sqrt{3}-15}{6}$