$\def\frac{\dfrac}$
1. $(\mathrm{CIE} 0606 / 2018 / \mathrm{w} / 11 / \mathrm{cg} 5)$
The diagram shows a circle with centre $O$ and radius $r \mathrm{~cm}$. The minor are $A B$ is such that angle $A O B$ is $\theta$ radians. The area of the minor sector $A O B$ is $48 \mathrm{~cm}^{2}$
(i) Show that $\theta=\frac{96}{x^{2}}$.
(ii) Given that the minor are $A B$ has length $12 \mathrm{~cm}$, find the value of $r$ and of $\theta$.
(iii) Using your values of $r$ and $\theta$, find the area of the shaded region.
2. (CIE $0606 / 2018 / \mathrm{w} / 12 / \mathrm{c} 11)$
The diagram shows the sector $O P Q$ of a circle, centre $O$, radius $\mathrm{rcm}$, where angle $P O Q=\theta$ radians. The perimeter of the sector is $10 \mathrm{~cm}$.
(i) Show that area, $A \mathrm{~cm}^{2}$, of the sector is given by $A=\frac{50 \theta}{(2+\theta)^{2}}$
It is given that $\theta$ can vary and $A$ has a maximum value.
(ii) Find the maximum value of $A$.
3. (CIE 0606/2018/w/13/ci2)
The diagram shows a sector $P O Q$ of a circle, centre $O$, radius $r \mathrm{~cm}$, where angle $P O Q=\theta$ radians. The perimeter of the sector is $20 \mathrm{~cm}$.
(i) Show that the area, $A \mathrm{~cm}^{2}$, of the sector is given by $A=10 r-r^{2}$.
It is given that $r$ can vary and that $A$ has a maximum value.
(ii) Find the value of $\theta$ for which $A$ has a maximum value.$[3]$
4. (CIE $0606 / 2019 / \mathrm{s} / 11 / \mathrm{q} 9)$
In this question all lengths are in centimetres.
A closed cylinder has base radius $r$, height $h$ and volume $V$. It is given that the total surface area of the cylinder is $600 \pi$ and that $V, r$ and $h$ can vary.
(i) Show that $V=300 \pi r-\pi r^{3}$.
(ii) Find the stationary value of $V$ and determine its nature.
5. (CIE $0606 / 2019 / \mathrm{w} / 11 / \mathrm{q} 9)$
The diagram shows a circle with centre $O$ and radius $10 \mathrm{~cm}$. The points $A, B, C$ and $D$ lie on the circle such that the chord $A B=15 \mathrm{~cm}$ and the chord $C D=10 \mathrm{~cm}$. The chord $A B$ is parallel to the chord $D C$.
(i) Show that the angle $A O B$ is $1.70$ radians correct to 2 decimal places.
(ii) Find the perimeter of the shaded region.
(iii) Find the area of the shaded region.$[4]$
6. (CIE $0606 / 2019 / \mathrm{w} / 12 / \mathrm{q} 10)$
The diagram shows a circle centre $O$, radius $10 \mathrm{~cm}$. The points $A, B$ and $C$ lie on the circumference of the circle such that $A B=B C=18 \mathrm{~cm}$.
(i) Show that angle $A O B=2.24$ radians correct to 2 decimal places.
(ii) Find the perimeter of the shaded region.$[5]$
(iii) Find the area of the shaded region.$[3]$
7. (CIE $0606 / 2019 / \mathrm{s} / 12 / \mathrm{q} 5)$
The diagram shows the right-angled triangle $O A B$. The point $C$ lies on the line $O B$. Angle $O A B=\frac{\pi}{2}$ radians and angle $A O B=\theta$ radians. $A C$ is an arc of the circle, centre $O$, radius $12 \mathrm{~cm}$ and $A C$ has length $9.6 \mathrm{~cm}$.
(i) Find the value of $\theta$.
(ii) Find the area of the shaded region.
8. (CIE 0606/2019/s/21/q8)
The diagram shows a right-angled triangle $A B C$ with $A B=8 \mathrm{~cm}$ and angle $A B C=\frac{\pi}{2}$ radians. The points $D$. and $E$ lie on $A C$ and $B C$ respectively. $B A D$ and $E C D$ are sectors of the circles with centres $A$ and $C$. respectively. Angle $B A D=\frac{2 \pi}{9}$ radians.
(i) Find the area of the shaded region.
(ii) Find the perimeter of the shaded region.$[3]$
9. (CIE 0606/2019/s/23/q7)
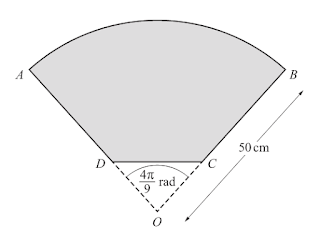
The diagram shows a company logo, $A B C D$. The logo is part of a sector, $A O B$, of a circle, centre $O$ and radius $50 \mathrm{~cm}$. The points $C$ and $D$ lic on $O B$ and $O A$ respectively, The lengths $A D$ and $B C$ are equal and $A D: A O$ is $7: 10 .$ The angle $A O B$ is $\frac{4 \pi}{9}$ radians.
(i) Find the perimeter of $A B C D$.$[5]$
(ii) Find the area of $A B C D$,$[3]$
10. (CIE $0606 / 2020 / \mathrm{s} / 11 / \mathrm{q} 7)$
The diagram shows an isosceles triangle $O A B$ such that $O A=O B$ and angle $A O B=\theta$ radians. The points $C$ and $D$ lie on $O A$ and $O B$ respectively. $C D$ is an arc of length $9.6 \mathrm{~cm}$ of the circle, centre $O .$ radius $12 \mathrm{~cm}$. The are $C D$ touches the line $A B$ at the point $M_{\text {. }}$
(a) Find the value of $\theta$.$[1]$
(b) Find the total area of the shaded regions.$[4]$
(c) Find the total perimeter of the shaded regions.$[3]$
11. (CIE $0606 / 2020 / \mathrm{s} / 12 / \mathrm{q} 11)$
The circles with centres $C_{1}$ and $C_{2}$ have equal radii of length $r \mathrm{~cm}$. The line $C_{1} C_{2}$ is a radius of both circles. The two circles intersect at $A$ and $B$.
(a) Given that the perimeter of the shaded region is $4 \pi \mathrm{cm}$, find the value of $r$.
(b) Find the exact area of the shaded region.
12. (CIE 0606/2020/w/12/q11)
In this question all lengths are in centimetres and all angles are in radians.
The diagram shows the rectangle $A D E F$, where $A F=D E=r$. The points $B$ and $C$ lie on $A D$ such that $A B=C D=r$. The curve $B C$ is an arc of the circle, centre $O$, radius $r$ and has a length of $1.5 r .$
(a) Show that the perimeter of the shaded region is $(7.5+2 \sin 0.75) r$.
(b) Find the area of the shaded region, giving your answer in the form $k r^{2}$, where $k$ is a constant correct to 2 decimal places.
13. (CIE $0606 / 2020 / \mathrm{s} / 13 / \mathrm{q} 7)$
At time $t \mathrm{~s}$, a particle travelling in a straight line has acceleration $(2 t+1)^{-\frac{1}{2}} \mathrm{~ms}^{-2}$. When $t=0$, the particle is $4 \mathrm{~m}$ from a fixed point $O$ and is travelling with velocity $8 \mathrm{~ms}^{-1}$ away from $O$.
(a) Find the velocity of the particle at time $t \mathrm{~s}$.
(b) Find the displacement of the particle from $O$ at time $t \mathrm{~s}$.$[4]$
14. (CIE $0606 / 2020 / \mathrm{w} / 13 / \mathrm{q} 8)$
In this question all lengths are in centimetres.
The diagram shows the figure $A B C$. The arc $A B$ is part of a circle, centre $O$, radius $r$, and is of length 1.45r. The point $O$ lies on the straight line $C B$ such that $C O=0.5 r$.
(a) Find, in radians, the angle $A O B$.$[1]$
(b) Find the area of $A B C$, giving your answer in the form $k r^{2}$, where $k$ is a constant.$[3]$
(c) Given that the perimeter of $A B C$ is $12 \mathrm{~cm}$, find the value of $r .$
15. (CIE 0606/2020/w/21/q12)
The diagram shows a shape consisting of two circles of radius $3 \mathrm{~cm}$ and $4 \mathrm{~cm}$ with centres $A$ and $B$. which are $5 \mathrm{~cm}$ apart. The circles intersect at $C$ and $D$ as shown. The lines $A C$ and $B C$ are tangents to the circles, centres $B$ and $A$ respectively. Find
(a) the angle $C A B$ in radians,
(b) the perimeter of the whole shape,$[4]$
(c) the area of the whole shape.$[4]$
16. (CIE $0606 / 2020 / \mathrm{s} / 22 / \mathrm{q} 11)$
The circles with centres $C_{1}$ and $C_{2}$ have equal radii of length $r \mathrm{~cm}$. The line $C_{1} C_{2}$ is a radius of both circles. The two circles intersect at $A$ and $B$.
(a) Given that the perimeter of the shaded region is $4 \pi \mathrm{cm}$, find the value of $r$.
(b) Find the exact area of the shaded region.$[4]$
17. (CIE $0606 / 2020 / \mathrm{m} / 22 / \mathrm{q} 6b)$
The diagram shows the sector $AOB$ of a circle with centre $O$ and radius 7 cm.
Angle $AOB = \frac{\pi}{4}$ radians. Find the perimeter of the shaded region. [3]
Answer
1. (i) Show
(ii) $r=8, \theta=1.5$
(iii) $16.1$
2. (i) Show
(ii) $A_{\max }=\frac{25}{4}$
3. (i) Show (ii) $\theta=2$
4. (i) Show
(ii) $2_{\max }=2000 \pi$
5. (i) Show
(ii) $P=60.4$ (iii) $A=270$
6. (i) Show (ii) $P=33.7$
(iii) $A=41.6$
7. (i) $\theta=0.8$
(ii) $A=16.5$
8. (i) $1.91$ (ii) $12.0$
9. (i) $p=159$ (ii) $A=1630$
10. (a) $\theta=0.8$
(b) Aren $=3.28$
(c) Perimeter $=21.8$
11. $y=-\frac{5}{4} \cos 2 x+2 x+5.53$
12. (a) prove
(b) $3.11 r^{2}$
13. (a) Prove
(b) perimeter $=19.2(\mathrm{c})$ Area $=11.4$
14. (a) $\angle A O B=1,45$ (radians)
(b) $0.973 \mathrm{r}^{2}$
(c) $r=2.91$
15. (a) $\angle C B A=0.927$
(b) $p=33.3$ (c) $A=71.9$
16. (a) $r=3$ (b) $A=6 \pi-\frac{9}{2} \sqrt{3}$
17. (a) $30 \pi$ (b) $10.9$














Post a Comment