| 1 | (IB/sl/2019/November/Paper1/q5)
[Maximum mark: 6] Consider the function $f$, with derivative $f^{\prime}(x)=2 x^{2}+5 k x+3 k^{2}+2$ where $x, k \in \mathbb{R}$.
|
| 2 | (IB/s1/2019/November/Paper1/48)
[Maximum mark: 14] A small cuboid box has a rectangular base of length $3 x \mathrm{~cm}$ and width $x \mathrm{~cm}$, where $x>0$. The height is $y \mathrm{~cm}$, where $y>0$. diagram not to scale The sum of the length, width and height is $12 \mathrm{~cm}$.
The volume of the box is $V \mathrm{~cm}^{3}$.
|
| 3 | (IB/sl/2019/November/Paper1/q10)
[Maximum mark: 14] Let $g(x)=p^{r}+q$, for $x, p, q \in \mathbb{R}, p>1$. The point $\mathrm{A}(0, a)$ lies on the graph of $g$. Let $f(x)=g^{-1}(x)$. The point B lies on the graph of $f$ and is the reflection of point A in the line $y=x$,
The line $L_{1}$ is tangent to the graph of $f$ at $\mathrm{B}$.
The line $L_{2}$ is tangent to the graph of $g$ at $\mathrm{A}$ and has equation $y=(\ln p) x+q+1$. The line $L_{2}$ passes through the point $(-2,-2)$. The gradient of the normal to $g$ at $\mathrm{A}$ is $\frac{1}{\ln \left(\frac{1}{3}\right)}$.
|
| 4 | $(\mathrm{IB} / \mathrm{s} 1 / 2019 /$ May $/$ paper $1 \mathrm{tz} 2 / \mathrm{q} 9)$
[Maximum mark: 15] Let $\theta$ be an obtuse angle such that $\sin \theta=\frac{3}{5}$
Let $f(x)=\mathrm{e}^{x} \sin x-\frac{3 x}{4}$.
The following diagram shows the graph of $f$ for $0 \leq x \leq 3$. Line $M$ is a tangent to the graph, of $f$ at point $\mathrm{P}$.
|
| 5 | (IB/s1/2019/May/paper2tz1/q4)
[Maximum mark: 8] Let $f^{\prime \prime}(x)=(\cos 2 x)(\sin 6 x)$, for $0 \leq x \leq 1 .$
|
| 6 | (IB/s1/2019/May/paper2tz1/q3)
[Maximum mark: 6] Consider the function $f(x)=x^{2} \mathrm{e}^{3 x}, x \in \mathbb{R}$.
|
| 7 | (IB/s1/2019/May/paper2tz2/q5)
[Maximum mark: 6] The population of fish in a lake is modelled by the function $f(t)=\frac{1000}{1+24 \mathrm{e}^{-0.3 t}}, 0 \leq t \leq 30$, where $t$ is measured in months.
|
| 8 | (IB/s1/2018/November/Paper1/q10)
[Maximum mark: 16] Let $f(x)=x^{3}-2 x^{2}+a x+6$. Part of the graph of $f$ is shown in the following diagram. The graph of $f$ crosses the $y$-axis at the point $\mathrm{P}$. The line $L$ is tangent to the graph of $f$ at $\mathrm{P}$.
(ii) Hence, find the equation of $L$ in terms of $a$. The graph of $f$ has a local minimum at the point $\mathrm{Q}$. The line $L$ passes through $\mathrm{Q}$.
|
| 9 | (IB/s1/2018/November/Paper2/q10)
[Maximum mark: 14] All lengths in this question are in metres. Consider the function $f(x)=\sqrt{\frac{4-x^{2}}{8}}$, for $-2 \leq x \leq 2 .$ In the following diagram, the shaded region is enclosed by the graph of $f$ and the $x$-axis. A container can be modelled by rotating this region by $360^{\circ}$ about the $x$-axis.
Water can flow in and out of the container. The volume of water in the container is given by the function $g(t)$, for $0 \leq t \leq 4$, where $t$ is measured in hours and $g(t)$ is measured in $\mathrm{m}^{3}$. The rate of change of the volume of water in the container is given by $g^{\prime}(t)=0.9-2.5 \cos \left(0.4 t^{2}\right)$.
When $t=0$, the volume of water in the container is $2.3 \mathrm{~m}^{3}$. It is known that the container is never completely full of water during the 4 hour period.
|
| 10 | $(\mathrm{IB} / \mathrm{s} 1 / 2018 /$ May $/$ paper $1 \mathrm{tz} 1 / \mathrm{q} 8)$
[Maximum mark: 13] A function $f(x)$ has derivative $f^{\prime}(x)=3 x^{2}+18 x$. The graph of $f$ has an $x$-intercept at $x=-1$.
|
| 11 | (IB/s1/2018/May/paper1tz2/q9)
[Maximum mark: 15] A closed cylindrical can with radius $r$ centimetres and height $h$ centimetres has a volume of $20 \pi \mathrm{cm}^{3}$. diagram not to scale
The material for the base and top of the can costs 10 cents per $\mathrm{cm}^{2}$ and the material for the curved side costs 8 cents per $\mathrm{cm}^{2}$. The total cost of the material, in cents, is $C$.
|
| 12 | (IB/s1/2018/May/paper1tz2/q10)
[Maximum mark: 16] Consider a function $f$. The line $L_{1}$ with equation $y=3 x+1$ is a tangent to the graph of $f$ when $x=2$.
Let $g(x)=f\left(x^{2}+1\right)$ and $\mathrm{P}$ be the point on the graph of $g$ where $x=1$.
|
| 13 | $(\mathrm{IB} / \mathrm{s} 1 / 2018 /$ May $/$ paper $2 \mathrm{tz} 1 / \mathrm{q} 1)$
[Maximum mark: 5] Let $f(x)=\ln x-5 x$, for $x>0$
|
| 14 | (IB/s1/2017/November/Paper1/q6)
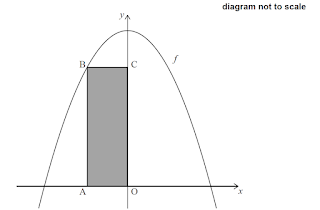
[Maximum mark: 7] Let $f(x)=15-x^{2}$, for $x \in \mathbb{R}$. The following diagram shows part of the graph of $f$ and the rectangle $\mathrm{OABC}$, where $\mathrm{A}$ is on the negative $x$-axis, $\mathrm{B}$ is on the graph of $f$, and $\mathrm{C}$ is on the $y$-axis. Find the $x$-coordinate of $\mathrm{A}$ that gives the maximum area of $\mathrm{OABC}$. |
| 15 | (IB/s1/2017/November/Paper2/q2)
[Maximum mark: 7] Let $f(x)=\frac{6 x^{2}-4}{\mathrm{e}^{x}}$, for $0 \leq x \leq 7$
|
| 16 | $(\mathrm{IB} / \mathrm{sl} / 2017 /$ May $/$ paper $1 \mathrm{tz} 1 / \mathrm{q} 6)$
[Maximum mark: 6] The following diagram shows the graph of $f^{\prime}$, the derivative of $f$. The graph of $f^{\prime}$ has a local minimum at $\mathrm{A}$, a local maximum at $\mathrm{B}$ and passes through $(4,-2)$
|
| 17 | $(\mathrm{IB} / \mathrm{s} 1 / 2017 /$ May $/$ paper $2 \mathrm{tz} 2 / \mathrm{q} 8)$
[Maximum mark: 15] Let $f(x)=-0.5 x^{4}+3 x^{2}+2 x$. The following diagram shows part of the graph of $f$. There are $x$-intercepts at $x=0$ and at $x=p$. There is a maximum at $\mathrm{A}$ where $x=a$, and $\mathrm{a}$, point of inflexion at B where $x=b$.
|
| 18 | (IB/s1/2016/November/Paper1/q10)
[Maximum mark: 16] Let $f(x)=\cos x$.
Let $g(x)=x^{k}$, where $k \in \mathbb{Z}$.
Let $k=21$ and $h(x)=\left(f^{(19)}(x) \times g^{(19)}(x)\right)$.
|
| 19 | (IB/s1/2016/November/Paper2/q2)
[Maximum mark: 7] Let $f(x)=0.225 x^{3}-2.7 x$, for $-3 \leq x \leq 3$. There is a local minimum point at $\mathrm{A}$.
|
| 20 | (IB/sl/2016/May/paper1tz1/q9)
[Maximum mark: 15] Let $f^{\prime}(x)=\frac{6-2 x}{6 x-x^{2}}$, for $0 < x < 6$ The graph of $f$ has a maximum point at $\mathrm{P}$.
The $y$-coordinate of $\mathrm{P}$ is $\ln 27$.
|
| 21 | (IB/s1/2016/May/paper1tz1/q10)
[Maximum mark: 15] Let $f(x)=\sqrt{4 x+5}$, for $x \geq-1.25$
Consider another function $g$. Let $\mathrm{R}$ be a point on the graph of $g$. The $x$-coordinate of $\mathrm{R}$ is 1 . The equation of the tangent to the graph at $\mathrm{R}$ is $y=3 x+6$.
|
| 22 | (IB/sl/2016/May/paper1tz2/q9)
[Maximum mark; 16] Fred makes an open metal container in the shape of a cuboid, as shown in the following diagram. The container has height $x \mathrm{~m}$, width $x \mathrm{~m}$ and length $y \mathrm{~m}$. The volume is $36 \mathrm{~m}^{3}$. Let $A(x)$ be the outside surface area of the container.
|
Answer
[1](a) Show (b) $-4\le x\le 4$
[2](a) $y=12-4x$ (b) $V=3x^2(12-4x)$ (c) $72x-36x^2$ (d)(i) $x=2$ (ii) $V''(2) < 0$ (e) $V=48$
[3](a) $B(a,0)$ (b) $y=\frac{1}{\ln(p)}(x-q-1)$ (c) $y=\frac{1}{\ln 3}(x-2\ln 3+2)$
[4](a) $-\frac{3}{4}$ (b) $ y=-\frac{3}{4}x $ (c) $e^x(\cos x+\sin x)-\frac{3}{4}$ (d) $\frac{3\pi}{4}$
[5](a) Figure (b) $\frac{\pi}{4}$ (c) $\frac{\pi}{6} < x < \frac{\pi}{4}$
[6](a) $f'(x)=2xe^{3x}+3x^2e^{3x}$ (b) $-\frac 23$
[7](a) 235 (b) 36 (c) $15.9$ months
[8](a) $(0,6)$ (b) (i) $f^{\prime}(x)=3 x^{2}-4 x+a$ (ii) $y=a x+6$ (c) $a=-4$
[9](a) $\frac{4 \pi}{3}$ (b)(i) $p=1.73, q=3.56$ (ii) $3.75$ (c) $0.331$
[10](a) $f(x)=x^{3}+9 x^{2}-8$ (b) $p=-3$ (c) $x < -3$
[11](a) $h=\frac{20}{r^{2}}$ (b) Show (c) $240 \pi$
[12](a)(i) 3 (ii) 7 (b) Show (c) $y=1$
[13](a) $f^{\prime}(x)=\frac{1}{x}-5$ (b) $f^{\prime \prime}(x)=-\frac{1}{x^{2}}$ (c) $x=0.558$
[14] $x=-\sqrt{5}$
[15](a) $\quad x=\sqrt{\frac{2}{3}}$ (b) $A(2.29,2.78)$ (c) Graph
[16](a) (i) $-2$ (ii) $x-2 y+2=0$ (b) Concave up $(4 < x < 5)$
[17](a) $p=2.73$ (b) (i) $(1.88,8.12)$ (ii) 0 (c) $(i)(1,4.5)$ (ii) 6 (d) $V=129$
[18](a)(i) $\quad f^{\prime}(x)=-\sin x, f^{\prime \prime}(x)=-\cos x, f^{\prime \prime \prime}(x)=\sin x, f^{\prime \prime}(x)=\cos x$ (ii) $f^{(19)}(x)=\sin x \quad$ (b) (i) $g^{\prime}(x)=k x^{k-1}, g^{\prime \prime}(x)=k(k-1) x^{k-2}$, $g^{\prime \prime \prime}(x)=k(k-1)(k-2) x^{k-3}$ (ii) $p=19$ (c) (i) $h^{\prime}(x)=\sin x(21 ! x)+\cos x\left(\frac{21 !}{2} x^{2}\right)$ (ii) Show
[19](a) $A(2,-3.6)$ (b) Graph
[20](a) $\quad x=3$ (b) $f(x)=\ln \left[3\left(6 x-x^{2}\right)\right]$ (c) $a=3, b=3$
[21](a) $f^{\prime}(1)=\frac{2}{3}$ (b) $g^{\prime}(1)=3$ (c) $g(1)=9$ (d) $y=15 x+12$
[22](a) Show (b) $A^{\prime}(x)=-\frac{108}{x^{2}}+4 x$ (c) 3 (d) 120











Post a Comment