$\def\iixi#1#2{\left(\begin{array}{c}#1\\#2\end{array}\right)}\let\frac=\dfrac$
| 1 | (IB/sl/2019/November/Paper2/q2)
[Maximum mark: 5] Consider the lines $L_{1}$ and $L_{2}$ with respective equations $$L_{1}: y=-\frac{2}{3} x+9 \text { and } L_{2}: y=\frac{2}{5} x-\frac{19}{5} .$$
A third line, $L_{3}$, has gradient $-\frac{3}{4}$
$L_{3}$ passes through the intersection of $L_{1}$ and $L_{2}$. (c) Write down a vector equation for $L_{3}$. [2] |
| 2 | (IB/sl/2016/November/Paper1/q7)
[Maximum mark: 7] Let $f(x)=m-\frac{1}{x}$, for $x \neq 0 .$ The line $y=x-m$ intersects the graph of $f$ in two distinct points. Find the possible values of $m$. |
| 3 | (IB/sl/2015/May/paper2tz2/q7)
[Maximum mark: 8] Let $f(x)=k x^{2}+k x$ and $g(x)=x-0.8$. The graphs of $f$ and $g$ intersect at two distinct points. Find the possible values of $k$. |
| 4 | (IB/sl/2019/May/paper1tz2/q6)
[Maximum mark: 7] Solve $\log _{4}(2-x)=\log _{16}(13-4 x)$. |
| 5 | (IB/sl/2018/November/Paper1/q4)
[Maximum mark: 6] Let $b=\log _{2} a$, where $a>0$. Write down each of the following expressions in terms of $b$.
|
| 6 | (IB/sl/2018/May/paper1tz2/q7)
[Maximum mark: 8] An arithmetic sequence has $u_{1}=\log _{c}(p)$ and $u_{2}=\log _{c}(p q)$, where $c>1$ and $p, q>0$.
|
| 7 | (IB/sl/2017/November/Paper1/q7)
[Maximum mark: 7] Consider $f(x)=\log _{x}\left(6 x-3 x^{2}\right)$, for $0 < x < 2$, where $k>0$. The equation $f(x)=2$ has exactly one solution. Find the value of $k$. |
| 8 | (IB/sl/2017/May/paper1tz2/q7)
[Maximum mark: 7] Solve $\log _{2}(2 \sin x)+\log _{2}(\cos x)=-1$, for $2 \pi < x < \frac{5 \pi}{2}$. |
| 9 | (IB/sl/2016/May/paper1tz2/q3)
[Maximum mark: 6] Let $x=\ln 3$ and $y=\ln 5$. Write the following expressions in terms of $x$ and $y$.
|
| 10 | (IB/sl/2015/May/paper1tz1/q3)
[Maximum mark: 6]
|
| 11 | (IB/sl/2016/May/paper2tz1/q7)
[Maximum mark: 8] Note: One decade is 10 years A population of rare birds, $P$, can be modelled by the equation $P_{0}=P_{3} \mathrm{e}^{\text {th }}$, where $P_{0}$ is the initial population, and $t$ is measured in decades. After one decade, it is estimated that $\frac{P_{1}}{P_{0}}=0.9$.
|
| 12 | (IB/sl/2019/November/Paper1/q2)
[Maximum mark: 6] In a class of 30 students, 18 are fluent in Spanish, 10 are fluent in French, and 5 are not fluent in either of these languages. The following venn diagram shows the events 'fluent in Spanish" and "fluent in French". The values $m, n, p$ and $q$ represent numbers of students.
|
| 13 | (IB/sl/2018/November/Paper2/q1)
[Maximum mark: 6] In a group of 35 students, some take art class $(A)$ and some take music class $(M) .5$ of these students do not take either class. This information is shown in the following Venn diagram.
|
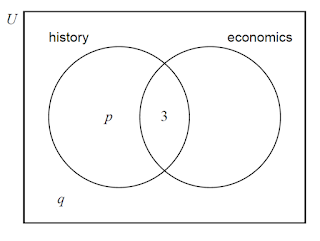
| 14 | (IB/sl/2017/May/paper1tz1/q1)
[Maximum mark: 6] In a group of 20 girls, 13 take history and 8 take economics. Three girls take both history and economics, as shown in the following venn diagram. The values $p$ and $q$ represent numbers of girls.
|
Answer
1](a) (12,1) (b) $\iixi{-4}{3}$ (c) $r=\iixi{12}{1} +t \iixi{-4}{3}$
2] $\quad m<-1$ or $m>1$
3] $k<0.2, k>5$
4] $ x=-3 $
5](a) $3 b$ (b) $3+b$ (c) $\frac{b}{3}$
6](a) show (b) 610
7] $k=\sqrt{3}$
8] $x=\frac{25 \pi}{12}, \frac{29 \pi}{12}$
9] (a) $y-x$ (b) $2 x+y$
10](a) $\quad m=3, n=4$ (b) $x=7.5$
11](a)(i) $\quad k=\ln 0.9$ (ii) population is decreasing (b) 28
12](a) 5 (b) 3 (c) 15,7
13](a) $17$ (b) (i) $\frac{18}{35}$ (ii) $\frac{24}{35}$
14](a)(i) $\quad p=10$ (ii) $q=2$ (b) $\frac{1}{4}$


Post a Comment