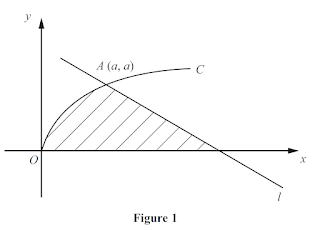
1. (2011/june/paper01/q5text)
The curve $C$, with equation $y^{2}=5 x$ and the line $l$ intersect at the point $A$ with coordinates $(a, a), a \neq 0$, as shown in Figure 1 .
(a) Find the value of $a$.
The line $l$ has gradient $-\frac{5}{7}$ and intersects the $x$-axis at the point $B$.
(b) Find the $x$-coordinate of $B$. (3)
The shaded region is rotated through $360^{\circ}$ about the $x$-axis.
(c) Find, in terms of $\pi$, the volume of the solid generated. $(5)$
2. (2011/june/Paper02/q11b)
Question 11 continued
The curve $C$ has equation $y=x^{2}+6 x+8$ and the line $l$ has equation $y=2-x$
In the space below,
(e) sketch, on the same axes, the curve $C$ and the line $l$.
(f) Find the area of the finite region bounded by the curve $C$ and the line $l$.
3. (2012/june/paper02/q5)
The curve $R$ has equation $y=x^{2}-7 x+10$
The curve $S$ has equation $y=-x^{2}+7 x-2$
(a) Find the coordinates of each of the two points where the curves $R$ and $S$ intersect.
(b) Find the area of the finite region bounded by the curve $R$ and the curve $S$.
4. (2013/june/paper01/q8text)
Figure 2 shows the curve $C$ with equation $y=15+2 x-x^{2}$
The curve crosses the $x$-axis at the points $A$ and $B$.
(a) Find the $x$-coordinate of $A$ and the $x$-coordinate of $B$.
(b) Use calculus to find the area of the finite region bounded by $C$ and the $x$-axis.
The line $l$ with equation $y=x+9$ intersects $C$ at the points $R$ and $S$.
(c) Find the $x$-coordinate of $R$ and the $x$-coordinate of $S$.
(d) Use calculus to find the area of the region bounded by $C$, the line $l$ and the $x$-axis, shown shaded in Figure 2 .
5. (2014/june/paper02/q7text)
Figure 2 shows the curve $C$ with equation $y^{2}=8(x-2)$ and the line $l$ with equation $y=x$ The line $l$ is the tangent to $C$ at the point $A$.
(a) Find the coordinates of $A$.
The region shown shaded in Figure 2 is rotated through $360^{\circ}$ about the $x$-axis.
(b) Use algebraic integration to find the volume of the solid formed.
Give your answer in terms of $\pi$. (5)
6. (2015/jan/paper01/q7text)
The curve $C$ has equation $y=x^{2}+3$
The point $A$ with coordinates $(0,3)$ and the point $B$ with coordinates $(4,19)$ lie on $C$, as shown below in Figure 3
The finite area enclosed by the arc $A B$ of curve $C$, the axes and the line with equation $x=4$ is rotated through $360^{\circ}$ about the $x$-axis.
(a) Using algebraic integration, calculate, to 1 decimal place, the volume of the solid generated.
(b) Using algebraic integration, calculate the area of the region between the chord $A B$ and the arc $A B$ of $C$, shown shaded in Figure 4 .
7. $(2015 /$ june $/$ paper02/q8text)
Figure 3 shows part of the curve $C$ with equation $y=x^{3}+a x^{2}+b x+c$
The curve passes through the origin $O$ and the points with coordinates $(2,0)$ and $(4,0)$.
(a) Show that $c=0$ (1)
(b) Find the value of $a$ and the value of $b$.
The point $P$ with $x$-coordinate 3 lies on $C$. The line $l$ passes through $O$ and meets $C$ at $P$.
(c) Show that $l$ is the tangent to $C$ at $P$.
The finite region $R$, shown shaded in Figure 3, is bounded by $C$ and by $l$.
(d) Use algebraic integration to find the area of $R$. (5)
8. (2016/jan/paper01/q9text)
Figure 2 shows the curve $S$ with equation $y=8-2 x-x^{2}$
The curve S crosses the $x$-axis at the points $A$ and $B_{.}$
(a) Find the $x$ coordinate of $A$ and the $x$ coordinate of $B .$ (3)
(b) Use calculus to find the area of the finite region bounded by $S$ and the $x$-axis.
The curve $T$ with equation $y=x^{2}+x+6$ intersects $S$
(c) Find the $x$ coordinates of the points of intersection of $S$ and $T .$
(d) Use calculus to find the area of the finite region bounded by $S$ and $T$. (4)
9. $(2016 / \mathrm{june} / \mathrm{paper} 02 / \mathrm{q} 6)$
(a) Use algebra to find the coordinates of the points of intersection of the curve with equation $y=x^{2}+2 x-6$ and the line with equation $y=5 x+4$
(b) Use algebraic integration to find the exact area of the finite region bounded by the curve and the line. (5)
10. (2017/june/paper02/q9text)
The curve $C$ with equation $y=x^{3}-4 x^{2}-4 x+16$ crosses the $x$-axis at the point with coordinates $(2,0)$ and at the points $A$ and $B$, as shown in Figure 1. The coordinates of the points $A$ and $B$ are $(a, 0)$ and $(b, 0)$ respectively.
(a) Find the value of $a$ and the value of $b$.
The point $D$ lies on $C$ and has $x$ coordinate 0
The line $l$ is the tangent to $C$ at the point $D .$
(b) Find an equation of $I$.
(c) Show that $l$ passes through $B$. $(1)$
(d) Use algebraic integration to find the area of the finite region bounded by $l$ and $C$. $(5)$
11. (2018/jan/paper02/q9text)
Figure 5 shows the curve $C$ with equation $y=x^{3}-2 x^{2}-5 x+6$
The curve $C$ crosses the $x$-axis at the points with coordinates $(-2,0),(a, 0)$ and $(b, 0)$
(a) (i) Show that $a=1$
(ii) Find the value of $b$. (4)
The point $P$ on $C$ has $x$ coordinate 2 and the line $l$ is the tangent to $C$ at $P$
(b) Show that $l$ crosses the $x$-axis at the point with coordinates $(-2,0)$
(c) Use algebraic integration to find the exact area of the finite region bounded by $C$ and $l .$ (4)
12. (2018/june/paper01/q8)
The line $l$ has equation $y+7 x=15$ and the curve $C$ has equation $y=x^{2}-6 x+9$
(a) Use algebra to find the coordinates of the points where $l$ intersects $C$.
(b) Use algebraic integration to find the exact area of the finite region bounded by $l$ and $C$.
13. (2019/juneR/paper01/q10)
$$\mathrm{f}(x)=6 x-x^{2} \quad x \in \mathbb{R}$$
Given that $\mathrm{f}(x)$ can be written in the form $D(x+E)^{2}+F$ where $D, E$ and $F$ are integers,
(a) find the value of $D$, the value of $E$ and the value of $F$. (3)
(b) Find
(i) the maximum value of $\mathrm{f}(x)$,
(ii) the value of $x$ for which the maximum occurs. (2)
The curve $C$ has equation $y=\mathrm{f}(x)$
The curve $S$ has equation $y=x^{2}-4 x+8$
The curve $S$ intersects the curve $C$ at two points.
(c) Find the coordinates of each of these two points,
The finite region $R$ is bounded by the curve $C$ and the curve $S$.
(d) Use algebraic integration to find the area of $R$.
Answer
1. (a) $\quad a=5$ (b) $x=12$ (c) $\frac{725}{6} \pi$
2. (b) (i) $-3$ (ii) $-1$ (c) $x=-6,-1$ (d) $x=-2, x=-4$ (e) Graph (f) $20 \frac{5}{6}$
3. (a) $(1,4),(6,4)$ (b) 41$\frac{2}{3}$
4. (a) $x=5,-3$ (b) $85 \frac{1}{3}$ (c) $x=3,-2$ (d) $64 \frac{1}{2}$
5. (a) $(4,4)$ (b) $\frac{16}{3} \pi$
6. (a) $1158.6$ (b) $10 \frac{2}{3}$
7. (a) Show (b) $a=-6, b=8$ (c) Show (d) $6 \frac{3}{4}$
8. (a) $x=-4, x=2$ (b) 36 (c) $x=\frac{1}{2},-2$ (d) $\frac{125}{24}$
9. (a) $(5,29),(-2,-6)$ (b) $57 \frac{1}{6}$
10. (a) $a=-2, b=4$ (b) $y=-4 x+16$ (d) $21 \frac{1}{3}$
11. (a)(i) Show (ii) $b=3$ (b) Show (c) $\frac{64}{3}$
12. (a) $(2,1),(-3,36)$ (b) $20\frac{5}{6}$
13. (a) $D=-1,E=-3,F=9$ (b)(i) $f(x)_{\max}=9$ (ii) $x=3$ (c) $(1,5), (4,8)$ (d) $A=9$







Post a Comment