$\def\D{\displaystyle}$
1 (CIE 2012, s, paper 12, question 8)

The figure shows a circle, centre $\D O,$ with radius 10 cm. The lines $\D XA$ and $\D XB$ are tangents to the circle at $\D A$ and $\D B$ respectively, and angle $\D AOB$ is $\D \frac{2\pi}{3}$ radians.
(i) Find the perimeter of the shaded region. [3]
(ii) Find the area of the shaded region. [4]
2 (CIE 2012, s, paper 21, question 11)
The diagram shows a right-angled triangle $\D ABC$ and a sector $\D CBDC$ of a circle with centre $\D C$ and radius 12 cm. Angle $\D ACB = 1$ radian and $\D ACD$ is a straight line.
(i) Show that the length of $\D AB$ is approximately 10.1 cm. [1]
(ii) Find the perimeter of the shaded region. [5]
(iii) Find the area of the shaded region. [4]
3 (CIE 2012, w, paper 12, question 8)
The diagram shows an isosceles triangle $\D OBD$ in which $\D OB = OD = 18$ cm and angle $\D BOD = 1.5$ radians. An arc of the circle, centre $\D O$ and radius 10 cm, meets $\D OB$ at $\D A$ and $\D OD$ at $\D C.$
(i) Find the area of the shaded region. [3]
(ii) Find the perimeter of the shaded region. [4]
4 (CIE 2012, w, paper 13, question 9)
The diagram shows four straight lines, $\D AD, BC, AC$ and $\D BD.$ Lines $\D AC$ and $\D BD$ intersect at $\D O$ such that angle $\D AOB$ is $\D \frac{\pi}{6}$ radians. $\D AB$ is an arc of the circle, centre $\D O$ and radius 10 cm, and $\D CD$ is an arc of the circle, centre $\D O$ and radius 20 cm.
(i) Find the perimeter of $\D ABCD.$ [4]
(ii) Find the area of $\D ABCD.$ [4]
5 (CIE 2012, w, paper 21, question 8)
In the diagram $\D PQ$ and $\D RS$ are arcs of concentric circles with centre $\D O$ and angle $\D POQ = 1$ radian. The radius of the larger circle is $\D x$ cm and the radius of the smaller circle is $\D y$ cm.
(i) Given that the perimeter of the shaded region is 20 cm, express $\D y$ in terms of $\D x.$ [2]
(ii) Given that the area of the shaded region is 16cm$\D^2,$ express $\D y^2$ in terms of $\D x^2.$ [2]
(iii) Find the value of $\D x$ and of $\D y.$ [4]
6 (CIE 2013, s, paper 11, question 8)
The diagram shows a square $\D ABCD$ of side 16 cm. $\D M$ is the mid-point of $\D AB.$ The points $\D E$ and $\D F$ are on $\D AD$ and $\D BC$ respectively such that $\D AE = BF = 6$ cm. $\D EF$ is an arc of the circle centre $\D M,$ such that angle $\D EMF$ is $\D \theta $ radians.
(i) Show that $\D \theta = 1.855$ radians, correct to 3 decimal places. [2]
(ii) Calculate the perimeter of the shaded region. [4]
(iii) Calculate the area of the shaded region. [3]
7 (CIE 2013, s, paper 22, question 6)
The shaded region in the diagram is a segment of a circle with centre $\D O$ and radius $\D r$ cm. Angle $\D AOB = \frac{\pi}{3}$ radians.
(i) Show that the perimeter of the segment is $\D r\left(\frac{3+\pi}{3}\right).$ [2]
(ii) Given that the perimeter of the segment is 26 cm, find the value of $\D r$ and the area of the
segment. [5]
8 (CIE 2013, w, paper 13, question 8)
The diagram shows two concentric circles, centre $\D O,$ radii 4 cm and 6 cm. The points $\D A$ and $\D B$ lie on the larger circle and the points $\D C$ and $\D D$ lie on the smaller circle such that $\D ODA$ and $\D OCB$ are straight lines.
(i) Given that the area of triangle $\D OCD$ is 7.5 cm$\D ^2,$ show that $\D \theta = 1.215$ radians, to 3 decimal places. [2]
(ii) Find the perimeter of the shaded region. [4]
(iii) Find the area of the shaded region. [3]
9 (CIE 2013, w, paper 21, question 10)
The diagram shows a circle with centre $\D O$ and a chord $\D AB.$ The radius of the circle is 12 cm andangle AOB is 1.4 radians.
(i) Find the perimeter of the shaded region. [5]
(ii) Find the area of the shaded region. [4]
10 (CIE 2014, s, paper 12, question 7)
The diagram shows a circle, centre $\D O,$ radius 8 cm. Points $\D P$ and $\D Q$ lie on the circle such that the chord $\D PQ = 12$ cm and angle $\D POQ = \theta$ radians.
(i) Show that $\D \theta = 1.696,$ correct to 3 decimal places. [2]
(ii) Find the perimeter of the shaded region. [3]
(iii) Find the area of the shaded region. [3]
11 (CIE 2014, s, paper 23, question 1)
The diagram shows a sector of a circle of radius $\D r$ cm. The angle of the sector is 1.6 radians and the area of the sector is 500 cm$\D ^2 .$
(i) Find the value of $\D r.$ [2]
(ii) Hence find the perimeter of the sector. [2]
12 (CIE 2014, w, paper 13, question 6)
The diagram shows a sector, $\D AOB,$ of a circle centre $\D O,$ radius 12 cm. Angle $\D AOB = 0.9$ radians. The point $\D C$ lies on $\D OA$ such that $\D OC = CB.$
(i) Show that $\D OC = 9.65$ cm correct to 3 significant figures. [2]
(ii) Find the perimeter of the shaded region. [3]
(iii) Find the area of the shaded region. [3]
13 (CIE 2014, w, paper 21, question 11)
The diagram shows a sector $\D OPQ$ of a circle with centre $\D O$ and radius $\D x$ cm. Angle $\D POQ$ is 0.8 radians. The point $\D S$ lies on $\D OQ$ such that $\D OS = 5$ cm. The point $\D R$ lies on $\D OP$ such that angle $\D ORS$ is a right angle. Given that the area of triangle $\D ORS$ is one-fifth of the area of sector $\D OPQ,$ find
(i) the area of sector $\D OPQ$ in terms of $\D x$ and hence show that the value of $\D x$ is 8.837 correct to 4 significant figures, [5]
(ii) the perimeter of $\D PQSR,$ [3]
(iii) the area of $\D PQSR.$ [2]
Answers
1. (i) $\D 55.6 $
(ii) $\D 68.5$
2. (ii) $\D 54.3$
(iii) $\D 187$
3. (i) $\D 86.6$
(ii) $\D 55.5$
4. (i) $\D 73.9,$
(ii) $\D 231$
5. (i) $\D y = 3x - 20$
(ii) $\D y^2 = x^2 -32$
(iii) $\D x = 9; y = 7$
6. (ii) $\D P = 54.6$
(iii) $\D A = 115.25$
7. (ii) $\D r = 12.7;A = 14.6$
8. (ii) $\D 15.9 $
(iii) $\D 14.4$
9. (i) $\D 74.1 $
(ii) $\D 422$
10. $\D P=48.7,A=178.5$
11. $\D 25; 90$
12. $\D P = 22.8;A = 19.4$
13. (ii) $\D P = 19.8;A = 25$
1 (CIE 2012, s, paper 12, question 8)

The figure shows a circle, centre $\D O,$ with radius 10 cm. The lines $\D XA$ and $\D XB$ are tangents to the circle at $\D A$ and $\D B$ respectively, and angle $\D AOB$ is $\D \frac{2\pi}{3}$ radians.
(i) Find the perimeter of the shaded region. [3]
(ii) Find the area of the shaded region. [4]
2 (CIE 2012, s, paper 21, question 11)
The diagram shows a right-angled triangle $\D ABC$ and a sector $\D CBDC$ of a circle with centre $\D C$ and radius 12 cm. Angle $\D ACB = 1$ radian and $\D ACD$ is a straight line.
(i) Show that the length of $\D AB$ is approximately 10.1 cm. [1]
(ii) Find the perimeter of the shaded region. [5]
(iii) Find the area of the shaded region. [4]
3 (CIE 2012, w, paper 12, question 8)
The diagram shows an isosceles triangle $\D OBD$ in which $\D OB = OD = 18$ cm and angle $\D BOD = 1.5$ radians. An arc of the circle, centre $\D O$ and radius 10 cm, meets $\D OB$ at $\D A$ and $\D OD$ at $\D C.$
(i) Find the area of the shaded region. [3]
(ii) Find the perimeter of the shaded region. [4]
4 (CIE 2012, w, paper 13, question 9)
The diagram shows four straight lines, $\D AD, BC, AC$ and $\D BD.$ Lines $\D AC$ and $\D BD$ intersect at $\D O$ such that angle $\D AOB$ is $\D \frac{\pi}{6}$ radians. $\D AB$ is an arc of the circle, centre $\D O$ and radius 10 cm, and $\D CD$ is an arc of the circle, centre $\D O$ and radius 20 cm.
(i) Find the perimeter of $\D ABCD.$ [4]
(ii) Find the area of $\D ABCD.$ [4]
5 (CIE 2012, w, paper 21, question 8)
In the diagram $\D PQ$ and $\D RS$ are arcs of concentric circles with centre $\D O$ and angle $\D POQ = 1$ radian. The radius of the larger circle is $\D x$ cm and the radius of the smaller circle is $\D y$ cm.
(i) Given that the perimeter of the shaded region is 20 cm, express $\D y$ in terms of $\D x.$ [2]
(ii) Given that the area of the shaded region is 16cm$\D^2,$ express $\D y^2$ in terms of $\D x^2.$ [2]
(iii) Find the value of $\D x$ and of $\D y.$ [4]
6 (CIE 2013, s, paper 11, question 8)
The diagram shows a square $\D ABCD$ of side 16 cm. $\D M$ is the mid-point of $\D AB.$ The points $\D E$ and $\D F$ are on $\D AD$ and $\D BC$ respectively such that $\D AE = BF = 6$ cm. $\D EF$ is an arc of the circle centre $\D M,$ such that angle $\D EMF$ is $\D \theta $ radians.
(i) Show that $\D \theta = 1.855$ radians, correct to 3 decimal places. [2]
(ii) Calculate the perimeter of the shaded region. [4]
(iii) Calculate the area of the shaded region. [3]
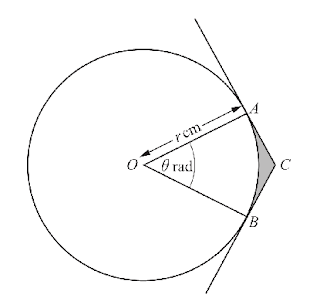
7 (CIE 2013, s, paper 22, question 6)
The shaded region in the diagram is a segment of a circle with centre $\D O$ and radius $\D r$ cm. Angle $\D AOB = \frac{\pi}{3}$ radians.
(i) Show that the perimeter of the segment is $\D r\left(\frac{3+\pi}{3}\right).$ [2]
(ii) Given that the perimeter of the segment is 26 cm, find the value of $\D r$ and the area of the
segment. [5]
8 (CIE 2013, w, paper 13, question 8)
The diagram shows two concentric circles, centre $\D O,$ radii 4 cm and 6 cm. The points $\D A$ and $\D B$ lie on the larger circle and the points $\D C$ and $\D D$ lie on the smaller circle such that $\D ODA$ and $\D OCB$ are straight lines.
(i) Given that the area of triangle $\D OCD$ is 7.5 cm$\D ^2,$ show that $\D \theta = 1.215$ radians, to 3 decimal places. [2]
(ii) Find the perimeter of the shaded region. [4]
(iii) Find the area of the shaded region. [3]
9 (CIE 2013, w, paper 21, question 10)
The diagram shows a circle with centre $\D O$ and a chord $\D AB.$ The radius of the circle is 12 cm andangle AOB is 1.4 radians.
(i) Find the perimeter of the shaded region. [5]
(ii) Find the area of the shaded region. [4]
10 (CIE 2014, s, paper 12, question 7)
The diagram shows a circle, centre $\D O,$ radius 8 cm. Points $\D P$ and $\D Q$ lie on the circle such that the chord $\D PQ = 12$ cm and angle $\D POQ = \theta$ radians.
(i) Show that $\D \theta = 1.696,$ correct to 3 decimal places. [2]
(ii) Find the perimeter of the shaded region. [3]
(iii) Find the area of the shaded region. [3]
11 (CIE 2014, s, paper 23, question 1)
The diagram shows a sector of a circle of radius $\D r$ cm. The angle of the sector is 1.6 radians and the area of the sector is 500 cm$\D ^2 .$
(i) Find the value of $\D r.$ [2]
(ii) Hence find the perimeter of the sector. [2]
12 (CIE 2014, w, paper 13, question 6)
The diagram shows a sector, $\D AOB,$ of a circle centre $\D O,$ radius 12 cm. Angle $\D AOB = 0.9$ radians. The point $\D C$ lies on $\D OA$ such that $\D OC = CB.$
(i) Show that $\D OC = 9.65$ cm correct to 3 significant figures. [2]
(ii) Find the perimeter of the shaded region. [3]
(iii) Find the area of the shaded region. [3]
13 (CIE 2014, w, paper 21, question 11)
The diagram shows a sector $\D OPQ$ of a circle with centre $\D O$ and radius $\D x$ cm. Angle $\D POQ$ is 0.8 radians. The point $\D S$ lies on $\D OQ$ such that $\D OS = 5$ cm. The point $\D R$ lies on $\D OP$ such that angle $\D ORS$ is a right angle. Given that the area of triangle $\D ORS$ is one-fifth of the area of sector $\D OPQ,$ find
(i) the area of sector $\D OPQ$ in terms of $\D x$ and hence show that the value of $\D x$ is 8.837 correct to 4 significant figures, [5]
(ii) the perimeter of $\D PQSR,$ [3]
(iii) the area of $\D PQSR.$ [2]
The diagram shows a circle, centre $O$, radius $12 \mathrm{~cm}$. The points $A, B$ and $C$ lie on the circumference of this circle such that angle $A O B$ is $1.7$ radians and angle $A O C$ is $2.4$ radians.
(i) Find the area of the shaded region.$[4]$
(ii) Find the perimeter of the shaded region.[5]
The diagram shows a circle, centre $O$, radius $8 \mathrm{~cm}$. The points $P$ and $Q$ lie on the circle. The lines $P T$ and $Q T$ are tangents to the circle and angle $P O Q=\frac{3 \pi}{4}$ radians.
(i) Find the length of $P T$.
(ii) Find the area of the shaded region.
(iii) Find the perimeter of the shaded region.
The diagram shows two circles, centres $A$ and $B$, each of radius $10 \mathrm{~cm}$. The point $B$ lies on the circumference of the circle with centre $A$. The two circles intersect at the points $C$ and $D$. The point $E$ lies on the circumference of the circle centre $B$ such that $A B E$ is a diameter.
(i) Explain why triangle $A B C$ is equilateral.$[1]$
(ii) Write down, in terms of $\pi$, angle $C B E$.
(iii) Find the perimeter of the shaded region.$[5]$
(iv) Find the area of the shaded region.[3]
The diagram shows an isosceles triangle $A B C$ such that $A C=10 \mathrm{~cm}$ and $A B=B C=6 \mathrm{~cm}$. $B X$ is an arc of a circle, centre $C$, and $B Y$ is an arc of a circle, centre $A$.
(i) Show that angle $A B C=1.970$ radians, correct to 3 decimal places.$[2$
(ii) Find the perimeter of the shaded region.$[4]$
(iii) Find the area of the shaded region.[3]
The diagram shows a circle, centre $O$, radius $r \mathrm{~cm}$. Points $A, B$ and $C$ are such that $A$ and $B$ lie on the circle and the tangents at $A$ and $B$ meet at $C$. Angle $A O B=\theta$ radians.
(i) Given that the area of the major sector $A O B$ is 7 times the area of the minor sector $A O B$, find the value of $\theta$
(ii) Given also that the perimeter of the minor sector $A O B$ is $20 \mathrm{~cm}$, show that the value of $r$, corred to 2 decimal places, is $7.18 .$
(iii) Using the values of $\theta$ and $r$ from parts (i) and (ii), find the perimeter of the shaded region $A B C$.$[3]$
(iv) Find the area of the shaded region $A B C$.[3]
The diagram shows a circle, centre $O$, radius $r \mathrm{~cm}$. The points $A$ and $B$ lie on the circle such that angle $A O B=2 \theta$ radians.
(i) Find, in terms of $r$ and $\theta$, an expression for the length of the chord $A B$.$[1]$
(ii) Given that the perimeter of the shaded region is $20 \mathrm{~cm}$, show that $r=\frac{10}{\theta+\sin \theta}$.[2]
(iii) Given that $r$ and $\theta$ can vary, find the value of $\frac{\mathrm{d} r}{\mathrm{~d} \theta}$ when $\theta=\frac{\pi}{6}$.[4]
(iv) Given that $r$ is increasing at the rate of $15 \mathrm{~cm} \mathrm{~s}^{-1}$, find the corresponding rate of change of 4 when $\theta=\frac{\pi}{6}$[3]
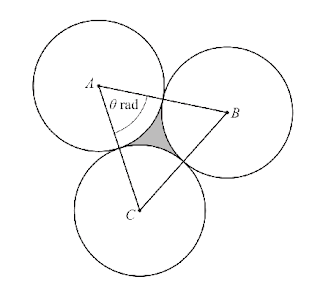
The diagram shows 3 circles with centres $A, B$ and $C$, each of radius $5 \mathrm{~cm}$. Each circle touches the other two circles. Angle $B A C$ is $\theta$ radians.
(i) Write down the value of $\theta$.$[1]$
(ii) Find the area of the shaded region between the circles.[4]
The diagram shows a sector of a circle with centre $O$ and radius $5 \mathrm{~cm}$. The length of the arc $A B$ is $7 \mathrm{~cm}$. Angle $A O B$ is $\theta$ radians.
(i) Explain why $\theta$ must be greater than 1 radian.$[1]$
(ii) Find the value of $\theta$.
(iii) Calculate the area of the sector $A O B$.[2]
(iv) Calculate the area of the shaded segment.[2]
The diagram shows a sector $A O B$ of the circle, centre $O$, radius $12 \mathrm{~cm}$, together with points $C$ and $D$ such that $A B C D$ is a rectangle. The angle $A O B$ is $\theta$ radians and the perimeter of the sector $A O B$ is $47 \mathrm{~cm}$
(i) Show that $\theta=1.92$ radians correct to 2 decimal places.$[2]$
(ii) Find the length of $C D$.$[2]$
(iii) Given that the total area of the shape is $425 \mathrm{~cm}^{2}$, find the length of $A D$.$[5]$
The points $A, B$ and $C$ lie on a circle centre $O$, radius $6 \mathrm{~cm}$. The tangents to the circle at $A$ and $C$ meet at the point $T$. The length of $O T$ is $10 \mathrm{~cm}$. Find
(i) the angle $\mathrm{TOA}$ in radians,
(ii) the area of the region $T A B C T$,
(iii) the perimeter of the region $T A B C T$.
The diagram shows a circle, centre $O$, radius $10 \mathrm{~cm}$. Points $A, B$ and $C$ lie on the circumference of the circle such that $A C=B C$. The area of the minor sector $A O B$ is $20 \pi \mathrm{cm}^{2}$ and angle $A O B$ is $\theta$ radians.
(i) Find the value of $\theta$ in terms of $\pi$.
(ii) Find the perimeter of the shaded region.$[4]$
(iii) Find the area of the shaded region.$[3]$
The diagram shows a circle, centre $O$, radius $12 \mathrm{~cm}$. The points $A$ and $B$ lie on the circumference of the circle and form a rectangle with the points $C$ and $D .$ The length of $A D$ is $8 \mathrm{~cm}$ and the area of the minor sector $A O B$ is $150 \mathrm{~cm}^{2}$.
(i) Show that angle $A O B$ is $2.08$ radians, correct to 2 decimal places.[2]
(ii) Find the area of the shaded region $A D C B$.$[6$
(iii) Find the perimeter of the shaded region $A D C B$.
The diagram shows a circle, centre $O$, radius $8 \mathrm{~cm}$. The points $A, B, C$ and $D$ lie on the circumference of the circle such that $A B$ is parallel to $D C$. The length of the arc $A D$ is $4 \mathrm{~cm}$ and the length of the chord $A B$ is $15 \mathrm{~cm}$.
(i) Find, in radians, angle $A O D .$$[1]$
(ii) Hence show that angle $D O C=1.43$ radians, correct to 2 decimal places.$[3]$
(iii) Find the perimeter of the shaded region.$[3]$
(iv) Find the area of the shaded region.[4]
The diagram shows a circle, centre $O$ of radius $r \mathrm{~cm}$, and a chord $A B$. Angle $A O B=\theta$ radians. The length of the major arc $A B$ is 5 times the length of the minor are $A B$. The minor are $A B$ has length $2 \pi \mathrm{cm}$.
(i) Find the value of $\theta$ and of $r$.
(ii) Calculate the exact perimeter of the shaded segment.
(iii) Calculate the exact area of the shaded segment.$[4]$
The diagram shows a circle, centre $A$, radius $10 \mathrm{~cm}$, intersecting a circle, centre $B$, radius $24 \mathrm{~cm}$. The two circles intersect at the points $P$ and $Q .$ The radii $A P$ and $A Q$ are tangents to the circle with centre $B$. The radii $B P$ and $B Q$ are tangents to the circle with centre $A$.
(i) Show that angle $P A Q$ is $2.35$ radians, correct to 3 significant figures.$[2]$
(ii) Find angle $P B Q$ in radians.[1]
(iii) Find the perimeter of the shaded region.$[3]$
(iv) Find the area of the shaded region.[4]
The diagram shows an isosceles triangle $A B C$, where $A B=A C=5 \mathrm{~cm}$. The arc $B E C$ is part of the circle centre $A$ and has length $6.2 \mathrm{~cm}$. The point $D$ is the midpoint of the line $B C$. The arc $B F C$ is semi-circle centre $D$.
(i) Show that angle $B A C$ is $1.24$ radians.$[1]$
(ii) Find the perimeter of the shaded region.[3]
(iii) Find the area of the shaded region.[4]
The diagram shows a circle, centre $O$, radius $10 \mathrm{~cm}$. The points $A, B, C$ and $D$ lie on the circumference of the circle such that $A B$ is parallel to $D C$. The length of the minor arc $A B$ is $14.8 \mathrm{~cm}$. The area of the minor sector $O D C$ is $21.8 \mathrm{~cm}^{2}$,
(i) Write down, in radians, angle $A O B$.[1]
(ii) Find, in radians, angle $D O C$.[2]
(iii) Find the perimeter of the shaded region.[4]
(iv) Find the area of the shaded region.$[3]$
The diagram shows a circle with centre $O$ and radius $8 \mathrm{~cm}$. The points $A, B, C$ and $D$ lie on the circumference of the circle. Angle $A O B=\theta$ radians and angle $C O D=1.4$ radians. The area of sector $A O B$ is $20 \mathrm{~cm}^{2}$
(i) Find angle $\theta$.$[2]$
(ii) Find the length of the arc $A B$.
(iii) Find the area of the shaded segment.[3]
In the diagram $A O B$ and $D O C$ are sectors of a circle centre $O$. The angle $A O B$ is $x$ radians. The length of the arc $A B$ is $40 \mathrm{~cm}$ and the radius $O B$ is $16 \mathrm{~cm}$.
(i) Find the value of $x$.$[2]$
(ii) Find the area of sector $A O B$.[2]
(iii) Given that the area of the shaded region $A B C D$ is $140 \mathrm{~cm}^{2}$, find the length of $O C$.[3]
In the diagram, $A B C$ is an arc of the circle centre $O$, radius $5 \mathrm{~cm}$, and angle $A O C$ is $1.5$ radians, $A D$ and $C E$ are diameters of the circle and $D E$ is a straight line.
(i) Find the total perimeter of the shaded regions.$[3]$
(ii) Find the total area of the shaded regions.$[3]$
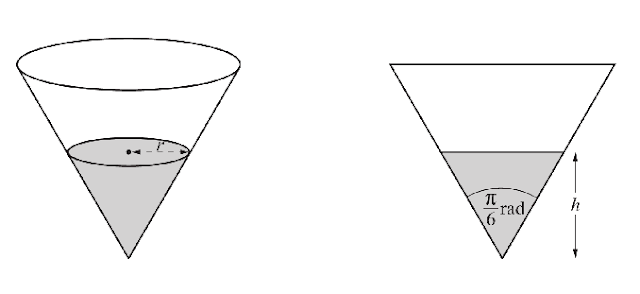
34 (CIE 2018, s, paper 22, question 12)
In this question all lengths are in centimetres.
The volume of a cone of height $h$ and base radius $r$ is given by $V=\frac{1}{3} \pi r^{2} h .$ It is known that $\sin \frac{\pi}{12}=\frac{\sqrt{6}-\sqrt{2}}{4}, \cos \frac{\pi}{12}=\frac{\sqrt{6}+\sqrt{2}}{4}, \tan \frac{\pi}{12}=2-\sqrt{3}$.
A water cup is in the shape of a cone with its axis vertical. The diagrams show the cup and its cross-section. The vertical angle of the cone is $\frac{\pi}{6}$ radians. The depth of water in the cup is $h .$ The surface of the water is a circle of radius $r$.
(i) Find an expression for $r$ in terms of $h$ and show that the volume of water in the cup is given by $V=\frac{\pi(7-4 \sqrt{3}) h^{3}}{3}$
(ii) Water is poured into the cup at a rate of $30 \mathrm{~cm}^{3} \mathrm{~s}^{-1}$. Find, correct to 2 decimal places, the rate at which the depth of water is increasing when $h=5 .$
1. (i) $\D 55.6 $
(ii) $\D 68.5$
2. (ii) $\D 54.3$
(iii) $\D 187$
3. (i) $\D 86.6$
(ii) $\D 55.5$
4. (i) $\D 73.9,$
(ii) $\D 231$
5. (i) $\D y = 3x - 20$
(ii) $\D y^2 = x^2 -32$
(iii) $\D x = 9; y = 7$
6. (ii) $\D P = 54.6$
(iii) $\D A = 115.25$
7. (ii) $\D r = 12.7;A = 14.6$
8. (ii) $\D 15.9 $
(iii) $\D 14.4$
9. (i) $\D 74.1 $
(ii) $\D 422$
10. $\D P=48.7,A=178.5$
11. $\D 25; 90$
12. $\D P = 22.8;A = 19.4$
13. (ii) $\D P = 19.8;A = 25$
14. (i) 181 (ii) $65.7$
15. $19.3,79.1,57.5$
16. (i)All sides are equal to the radii
of the circles which are also equal
(ii) $2 \pi / 3$ (iii) $58.3$ (iv) 148
17. (ii) $9.03$ (iii) $4.50$
18. (i) $\theta=\pi / 4$
(ii) $r=7.180$
(iii) $11.6$
(iv) $1.08 \leq$ Area $\leq 1.11$
19. (i) $r \sin 2 \theta / \cos \theta$
(iii) -17.8 (iv) - $0.842$
20. (i) $\pi / 3$
(ii) $25 \sqrt{3}-25 \pi / 2$
21. (ii) $1.4$ (iii) $17.5$ (iv) $5.18$
22. (ii) $19.6($ iii $) 18.1$
23. $0.927,128,42.6$
24. (i) $2 \pi / 5$, (ii) $50.6(\mathrm{iii}) 122$
25. $2.08,78.4,61.7$
26. (i) $0.5$ (ii) $1.43$
(iii) $33.5$ (iv) $42.8$
27. (i) $\pi / 3,6$
(ii) $10 \pi+6$
(iii) $30 \pi+9 \sqrt{3}$
28. (i) $2.352$ (ii) $0.790$
(iii) $42.5$ (iv) 105
29. (i) $1.24$ (ii) $15.3$
(iii) $9.58 \leq$ Area $\leq 9.62$
30. (i) $1.48$, (ii) $0.436$
(iii) $54.7$ (iv) 178
31. $5 / 8,5,13.3$
32. $x=2.5,320,12$
33. (i) $34.31-34.32$
(ii) $31.21-31.22$
34. (ii) $5.32$






























please tell how to solve the 7 (i)
ReplyDeleteYou have to show the triangle is equilateral. Or otherwise you use cosine rule. Then you get the length of line segment is r. Moreover the arc length is r\pi/3. Thus perimeter=r+r\pi/3.
DeleteCenter angle=60, sum of the rest angle is 180-60=120. Thus each=120/2=60.
DeletePost a Comment