$\def\vecab{\overrightarrow}$
$\def\D{\displaystyle}$
$\def\frac{\dfrac}$
$\def\rbox#1#2{\begin{array}{|#1|}\hline #2\\ \hline\end{array}}$
$\let\rtable=\rbox$
$\def\matrix#1{\left(\begin{array}{ccc}#1\end{array}\right)}$
$\def\fbox#1{\begin{array}{|l|}\hline #1\\ \hline\end{array}}$
$\let\cvec=\matrix$
$\let\ruletable=\rbox$
$\def\tbox#1{\begin{array}{|l|}\hline \mbox{#1}\\ \hline\end{array}}$
$\def\dint{\displaystyle\int}\def\dlim{\displaystyle\lim}$
$\def\dsum{\displaystyle\sum}$
$\def\mathrm{}$
$\newcommand{\inside}[2]{\begin{array}{rcl}\leftarrow-- & \circ\!\frac{\qquad\qquad\qquad\qquad}{}\!\circ & --\rightarrow\\ & #1\qquad\qquad\qquad\qquad #2 & \end{array}}$
$\newcommand{\insideeq}[2]{\begin{array}{rcl}\leftarrow--&\bullet\!\frac{\qquad\qquad\qquad\qquad}{}\!\bullet & --\rightarrow\\& #1\qquad\qquad\qquad\qquad #2&\end{array}}$
$\newcommand{\outside}[2]{\begin{array}{rcl}\leftarrow\!\!\!\frac{\qquad\qquad}{}\!\circ & ---- &\circ\!\frac{\qquad\qquad}{}\!\!\!\rightarrow\\#1& & #2\end{array}}$
$\newcommand{\outsideeq}[2]{\begin{array}{rcl}\leftarrow\!\!\!\frac{\qquad\qquad}{}\!\bullet & ---- &\bullet\!\frac{\qquad\qquad}{}\!\!\!\rightarrow\\#1& & #2\end{array}}$
$$ \begin{gathered} f(x)=k x-1, g(x)=x+12 \\ (g \circ f)(2)=(f \circ g)(2) \\ g(f(2))=f(g(2)) \\ g(2 k-1)=f(14) \\ 2 k-1+12=14 k-1 \\ 12 k=12 \\ \therefore k=1 \end{gathered} $$
Let $f(x)=x^{3}+p x^{2}-8 q x+5$ and $g(x)=2 x^{3}-q x^{2}+4 p x-18.$
Since $x-2$ is a common factor of $f(x)$ and $g(x)$, $$ \begin{aligned} \therefore f(2)=0 & \text { and } \quad g(2)=0 \\ 8+4 p-16 q+5 &=0 \\ 4 p-16 q &=-13 &\qquad (1)\\ g(2) &=0 \\ 16-4 q+8 p-18 &=0 \\ 8 p-4 q &=2 \\ 4 p-2 q &=1&\qquad (2) \end{aligned} $$ $$\begin{array}{rll} \text{Eq. (1)}\rightarrow 4 p-16 q&=-13&\cdots (3)\\ \text{Eq. (2)}\rightarrow 4 p-2 q&=1&\cdots (4)\\ (3)-(4):& -14 q=-14\end{array}$$ $\therefore q=1$, and Substitute $q=1$ in Eq. (2), $$ \begin{array}{r} 4 p-2=1 \\ 4 p=3 \\ \therefore p=\frac{3}{4} \\ \therefore p=\frac{3}{4}, q=1 \end{array} $$
\begin{aligned} &\quad \text { In an A.P., } \quad u_{p}=q, u_{q}=p \text {. }\\ &\begin{array}{r} u_{p}=q \\ a+(p-1) d=q&\cdots(1) \end{array}\\ & a+p d-d=q\\ & u_{q}=p\\ & a+(q-1) d=p\\ & a+q d-d=p&\cdots(2)\\ &\text { Eq. (1) } \rightarrow \quad a+p d-d=q&\cdots(3)\\ &\text { Eq. (2) } \rightarrow a+q d-d=p&\cdots(4)\\ &(3)-(4):(p-q) d=-(p-q)\\ &\therefore d=-1\\ & u_{p+q}=a+(p+q-1) d\\ &=a+p d+q d-d\\ &=a+p d-d+q d\\ &=q+q d\\ &=q+q(-1)\\ &\therefore u_{p+q}=0 \end{aligned}
$$\begin{array}{rr}\text { In a G.P, } & u_{1}-u_{2}=2 \\ & a-a r=2 \\ & a(1-r)=2 &\cdots (1)\\ & S=50\\ &\frac{a}{1-r}=50 & \cdots (2)\\ (1)\times (2):& a^2=100\\& a=\pm 10\end{array}$$ If $a=-10, 1-r=\frac{2}{-10}$. Thus $r=\frac 65$, which is impossible because $|r| < 1.$ Thus $a=10$.
Given: $O$ is the centre of the circle
To find: $\angle R Q T$
$$
\begin{aligned}
&\text { Solution: } \beta=90^{\circ}(\because \text { radius } \perp \text { tangent }) \\
&\qquad \begin{aligned}
\delta &=\beta+34^{\circ}=124^{\circ} \\
\alpha &=\frac{\delta}{2}=\frac{124^{\circ}}{2}=62^{\circ} \\
\therefore & \angle R Q T=\alpha=62^{\circ}
\end{aligned}
\end{aligned}
$$
\begin{aligned} \sin 2 x(1+2 \cos x) &=\sin 2 x+2 \sin 2 x \cos x\\ &=\sin 2x+\left(\sin(2x+x)+\sin(2x-x)\right)\\ &=\sin 2x+\sin 3x+\sin x\\ &=\sin x+\sin 2 x+\sin 3 x \end{aligned}
\begin{aligned} &\lim _{x \rightarrow 2} \frac{x^{3}-8}{\sqrt{x+2}-2}\\ &=\lim _{x \rightarrow 2} \frac{(x-2)\left(x^{2}+2 x+4\right)}{\sqrt{x+2}-2} \times \frac{\sqrt{x+2}+2}{\sqrt{x+2}+2}\\ &=\lim _{x \rightarrow 2} \frac{(x-2)\left(x^{2}+2 x+4\right)(\sqrt{x+2}+2)}{x+2-4}\\ &=\lim _{x \rightarrow 2} \frac{(x-2)\left(x^{2}+2 x+4\right)(\sqrt{x+2}+2)}{x-2}\\ &=\lim _{x \rightarrow 2}\left[\left(x^{2}+2 x+4\right)(\sqrt{x+2}+2)\right]\\ &=\left(2^{2}+2(2)+4\right)(\sqrt{2+2}+2)\\ &=12 \times 4\\ &=48 \end{aligned} \begin{aligned} &\lim _{x \rightarrow 0} \frac{\cos x-1}{\sin ^{2} x} \\ =& \lim _{x \rightarrow 0} \frac{\cos x-1}{1-\cos ^{2} x} \\ =& \lim _{x \rightarrow 0} \frac{\cos x-1}{(1+\cos x)(1-\cos x)} \\ =& \lim _{x \rightarrow 0} \frac{-(1-\cos x)}{(1+\cos x)(1-\cos x)} \\ =& \lim _{x \rightarrow 0} \frac{-1}{1+\cos x} \\ =& \frac{-1}{1+\cos 0} \\ =& \frac{-1}{1+1} \\ =&-\frac{1}{2} \end{aligned}
\begin{aligned} f(x) &=\frac{x}{x-3}, x \neq 3, g(x)=3 x+5 \\ (f\circ g)^{-1}(x)&=\frac 53\\ x& =(f\circ g)\left(\frac{5}{3} \right)\\ & =f \left(g\left(\frac{5}{3} \right)\right)\\ & =f \left(3\times \left(\frac{5}{3} \right)+5\right)\\ &=f(10)\\ & \therefore x=\frac{10}{10-3}=\frac{10}{7} \\ \end{aligned}
$\odot$ is not a binary operation.
Let $f(x)=x^{3}-a x-6$ $x+2$ is a factor of $f(x)$ $$ \begin{aligned} f(-2) &=0 \\ (-2)^{3}-a(-2)-6 &=0 \\ -8+2 a-6 &=0 \\ 2 a &=14 \\ \therefore a &=7 \end{aligned} $$ Let $g(x)=2 x^{3}+a x^{2}-6 x+9$
When $g(x)$ is divided by $x+1$, the remainder $=g(-1)$ $$ \begin{aligned} &=2(-1)^{3}+7(-1)^{2}-6(-1)+9 \\ &=-2+7+6+9 \\ &=20 \end{aligned} $$
$-7+(2 x+1)^{2} \geq 6 x$
$-7+4 x^{2}+4 x+1-6 x \geq 0$
$4 x^{2}-2 x-6 \geq 0$
$2 x^{2}-x-3 \geq 0$
$(x+1)(2 x-3) \geq 0$
$x+1 \leq 0$ and $2 x-3 \leq 0$ (or) $x+1 \geq 0$ and $2 x$
$x \leq-1$ and $x \leq \frac{3}{2}$ (or) $x \geq-1$ and $x \geq \frac{3}{2}$
$x \leq-1$ (or) $x \geq \frac{3}{2}$
The solution set $=\left\{x \mid x \leq-1\right.$ (or) $\left.x \geq \frac{3}{2}\right\}$
$\outsideeq{-1}{\frac 32}$
$b, x, y, c$ are consecutive terms of a G.P. Let $r=$ common ratio. $$ \therefore x=b r, y=b r^{2}, c=b r^{3} $$ The A.M. between $b$ and $c$ is $a$. $$ \begin{aligned} \frac{b+c}{2} &=a \\ b+c &=2 a \\ x^{3}+y^{3} &=b^{3} r^{3}+b^{3} r^{6} \\ &=\left(b^{2}+b^{2} r^{3}\right) b r^{3} \\ &=\left(b+b r^{3}\right) b c \\ &=(b+c) b c \\ \therefore x^{3}+y^{3} &=2 a b c \end{aligned} $$
In a G.P., $$\begin{array}{rll} u_{1} \times u_{2} \times u_{3}&=1000\\ a \times a r \times a r^{2}&=1000\\ a^{3} r^{3}&=1000\\ a r&=10&\cdots (1)\end{array}$$ $u_{1} ,u_{2}+6, u_{3}+7$ is an A.P.
$a, a r+6, a r^{2}+7$ is an A.P. $$\begin{array}{rll} a r+6-a&=a r^{2}+7-(a r+6)\\ 10+6-a&=10 r+7-16 \quad(\because a r=10)\\ 16-a &=10 r-9\\ a &=25-10 r\end{array}$$ Substitute $a=25-10 r$ in Eq. (1), $$ \begin{array}{r} (25-10 r) r=10 \\ 25 r-10 r^{2}-10=0 \\ 10 r^{2}-25 r+10=0 \\ 2 r^{2}-5 r+2=0 \\ (2 r-1)(r-2)=0 \\ r=\frac{1}{2}(\text { or }) r=2 \end{array} $$ When $r=\frac{1}{2}, a=20$
The first three terms of the GP. are $20,10,5$.
When $r=2, a=5$.
The first three terms of the G.P. are $5,10,20$
$$ \begin{aligned} & A=\left(\begin{array}{cc} 4 & 1 \\ -9 & -2 \end{array}\right), B=\left(\begin{array}{cc} -3 & 1 \\ -1 & 2 \end{array}\right) \\ &\operatorname{det} A=-8-(-9)=1, A^{-1} \text { exists } \\ & A^{-1}=\frac{1}{\operatorname{det} A}\left(\begin{array}{cc} -2 & -1 \\ 9 & 4 \end{array}\right)=\frac{1}{1}\left(\begin{array}{cc} -2 & -1 \\ 9 & 4 \end{array}\right)=\left(\begin{array}{cc} -2 & -1 \\ 9 & 4 \end{array}\right) \\ & A^{2}=\left(\begin{array}{cc} 4 & 1 \\ -9 & -2 \end{array}\right)\left(\begin{array}{cc} 4 & 1 \\ -9 & -2 \end{array}\right)=\left(\begin{array}{cc} 16-9 & 4-2 \\ -36+18 & -9+4 \end{array}\right)=\left(\begin{array}{cc} 7 & 2 \\ -18 & -5 \end{array}\right) \\ & A X=2 B-A^{2}=\left(\begin{array}{cc} -6 & 2 \\ -2 & 4 \end{array}\right)-\left(\begin{array}{cc} 7 & 2 \\ -18 & -5 \end{array}\right)=\left(\begin{array}{cc} -13 & 0 \\ 16 & 9 \end{array}\right) \\ & A X=\left(\begin{array}{cc} -13 & 0 \\ 16 & 9 \end{array}\right) \\ & X=A^{-1}\left(\begin{array}{cc} -13 & 0 \\ 16 & 9 \end{array}\right)=\left(\begin{array}{cc} -2 & -1 \\ 9 & 4 \end{array}\right)\left(\begin{array}{cc} -13 & 0 \\ 16 & 9 \end{array}\right)=\left(\begin{array}{cc} 26-16 & -9 \\ -117+64 & 36 \end{array}\right) \\ &\therefore X=\left(\begin{array}{cc} 10 & -9 \\ -53 & 36 \end{array}\right) \end{aligned}$$
\begin{aligned} &\text{Let } A=\left(\begin{array}{cc} 1 & 1 \\ -1 & 1 \end{array}\right)\\ &\det A=1-(-1)=2 \\ & A^{-1}=\frac{1}{\det A}\left(\begin{array}{ll} 1 & -1 \\ 1 & 1 \end{array}\right)=\frac{1}{2}\left(\begin{array}{ll} 1 & -1 \\ 1 & 1 \end{array}\right) \end{aligned} \begin{aligned} y-x&=1 \\ x+y&=3 \\ x+y&=3 \\ -x+y&=1 \\ \left(\begin{array}{ll} 1 & 1 \\ -1 & 1 \end{array}\right)\left(\begin{array}{l} x \\ y \end{array}\right)&=\left(\begin{array}{l} 3 \\ 1 \end{array}\right) \\ \left(\begin{array}{ll} x \\ y \end{array}\right)&=\left(\begin{array}{cc} 1 & 1 \\ -1 & 1 \end{array}\right)^{-1}\left(\begin{array}{l} 3 \\ 1 \end{array}\right)\\&=\frac{1}{2}\left(\begin{array}{ll} 1 & -1 \\ 1 & 1 \end{array}\right)\left(\begin{array}{l} 3 \\ 1 \end{array}\right)\\&=\frac{1}{2}\left(\begin{array}{l} 3-1 \\ 3+1 \end{array}\right)=\frac{1}{2}\left(\begin{array}{l} 2 \\ 4 \end{array}\right)=\left(\begin{array}{l} 1\\ 2 \end{array}\right)\\ \text{Thus }& x=1,y=2. \end{aligned}
Number of possible outcomes $=8$
(i) only the first child is a boy
The set of favourable outccmes $=\{$ (B,G,G) $\}$
Number of favourable outcomes $=1$
$\therefore \mathrm{P}($ only the first child is a boy $)=\frac{1}{8}$
(ii) the last child is a boy
The set of favourable outcomes $=\{(\mathrm{B}, \mathrm{B}, \mathrm{B}),(\mathrm{B}, \mathrm{G}, \mathrm{B}),(\mathrm{G}, \mathrm{B}, \mathrm{B}),(\mathrm{G}, \mathrm{G}, \mathrm{B})\}$
Number of favourable outcomes $=4$
$\therefore \mathrm{P}($ the last child is a boy $)=\frac{4}{8}=\frac{1}{2}$
(iii) the last two children born are boys
The set of favourable outcomes $=\{(\mathrm{B}, \mathrm{B}, \mathrm{B}),(\mathrm{G}, \mathrm{B}, \mathrm{B})\}$
Number of favourable outcomes $=2$
$\therefore P($ the last two children born are boys $)=\frac{2}{8}=\frac{1}{4}$
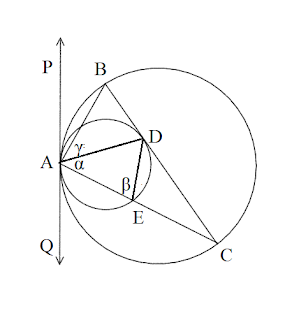
Prove: $A D$ bisects $\angle B A C$.
Proof: Draw a common tangent $P A Q$ at $A$. Join $D E$.
tangent to the smaller circle at $D$.
Proof: Draw a common tangent $P A Q$ at $A$. Join $D E$.
$\angle C D E=\alpha \quad($ Theorem 4$)$
$\angle P A B=\angle C \quad($ Theorem 4$)$
$\angle C D E+\angle C=\beta ($ Exterior $\angle$ of $\Delta C D E)$
$\angle P A D=\beta \quad($ Theorem 4$)$
$\therefore \angle P A B+\gamma=\angle C D E+\angle C$
$\angle C+\gamma=\alpha+\angle C$
$\therefore \quad \gamma=\alpha$
$\therefore A D$ bisects $\angle B A C .$
Given : $P V$ is tangent and $Q T / / P V$.
Prove: $Q R S T$ is cyclic.
Proof: $\gamma=\beta$ (Theorem 4 )
$\begin{aligned} \alpha &=\beta \\ \therefore \alpha &=\gamma \end{aligned}$
$\alpha+\delta=180^{\circ}$
$\therefore \gamma +\delta=180^{\circ}$
$\therefore Q R S T$ is cyclic.
Given : $\ln \triangle A B C, A D \perp B C, B E \perp A C, \angle A C D=45^{\circ}$
Prove: $\alpha(\triangle D E C): \alpha(\triangle A B C)=1: 2$
Proof: $\angle A D B=\angle A E B=90^{\circ}$
$\therefore A B D E$ is cyclic.
$\therefore \angle D E C=\angle A B C$
$\ln \triangle D E C$ and $\triangle A B C$ $$\begin{aligned} \angle D E C &=\angle A B C \quad \text { (proved) } \\ \angle C &=\angle C \\ \triangle D E C & \sim \triangle A B C \quad \text { (AA) } \end{aligned}$$ $$\begin{array}{rll} \frac{\alpha(\Delta D E C)}{\alpha(\Delta A B C)}&=\frac{D C^{2}}{A C^{2}}\\&=\left(\frac{D C}{A C}\right)^{2}\\&=\left(\cos 45^{\circ}\right)^{2}\\ &=\left(\frac{1}{\sqrt{2}}\right)^{2}=\frac{1}{2}\end{array}$$ $\therefore \alpha(\Delta D E C): \alpha(\Delta A B C)=1: 2$
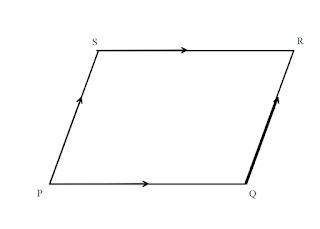
$\def\vecAB#1{\overrightarrow{#1}}$
$\overrightarrow{O P}=\left(\begin{array}{l}1 \\ 3\end{array}\right), \overrightarrow{O Q}=\left(\begin{array}{l}5 \\ 4\end{array}\right), \overrightarrow{O R}=\left(\begin{array}{l}1 \\ 9\end{array}\right)$
$P Q R S$ is a parallelogram. $$\begin{array}{rl} \vecAB{PQ}&=\vecAB{SR}\\ \vecAB{OQ}-\vecAB{OP}&=\vecAB{OR}-\vecAB{OS}\\ \left(\begin{array}{l}5 \\ 4\end{array}\right)-\left(\begin{array}{l}1 \\ 3\end{array}\right)&=\left(\begin{array}{l}1 \\ 9\end{array}\right)-\overrightarrow{O S}\\ \left(\begin{array}{l}4 \\ 1\end{array}\right)&=\left(\begin{array}{l}1 \\ 9\end{array}\right)-\overrightarrow{O S}\\ \overrightarrow{O S}&=\left(\begin{array}{l}1 \\ 9\end{array}\right)-\left(\begin{array}{l}4 \\ 1\end{array}\right)\\ \overrightarrow{O S}&=\left(\begin{array}{r}-3 \\ 8\end{array}\right) \end{array}$$ $\therefore$ The coordinates of $S$ is $(-3,8)$.
$$\begin{array}{rcl} \frac{1+\tan ^{2} \alpha}{2-\sec ^{2} \alpha} &=&\frac{\sec ^{2} \alpha}{2-\sec ^{2} \alpha} \times \frac{\div \sec^2\alpha}{\div \sec^2\alpha}\\ &=&\frac{1}{\left(\frac{2}{\sec ^{2} \alpha} -1\right)}\\ &=&\frac{1}{2 \cos ^{2} \alpha-1} \\ &=&\frac{1}{\cos 2 \alpha} \\ &=&\sec 2 \alpha \end{array}$$
$$
\begin{aligned}
\angle P Q R &=35^{\circ}+42^{\circ} 12^{\prime}=77^{\circ} 12^{\prime} \\
P R^{2} &=P Q^{2}+Q R^{2}-2 \times P Q \times Q R \cos \angle P Q R \\
&=50^{2}+68^{2}-2 \times 50 \times 68 \cos 77^{\circ} 12^{\prime} \\
&=2500+4624-6800 \cos 77^{\circ} 12^{\prime} \\
&=7124-1507 \\
&=5617 \\
\therefore P R &=74.95 \mathrm{~km}
\end{aligned}
$$
$\therefore$ Distance of $P$ from $R$ is $74.95 \mathrm{~km}$.
$$\begin{aligned} & \frac{\sin \gamma}{P Q}=\frac{\sin \angle P Q R}{P R} \\ \sin \gamma &=\frac{50 \times \sin 77^{\circ} 12^{\prime}}{74.95} \\ \sin \gamma &=\sin 40^{\circ} 35^{\prime} \\ \gamma &=40^{\circ} 35^{\prime} \\
&\text{Since }\alpha= 42^{\circ} 12^{\prime},\\
\gamma+\alpha &=40^{\circ} 35^{\prime}+42^{\circ} 12^{\prime}=82^{\circ} 47^{\prime} \\ &\therefore \quad \text { Bearing of } P \text { from } R \text { is } \mathrm{S} 82^{\circ} 47^{\prime} \mathrm{E} . \end{aligned}$$
$$\begin{array}{r|l}
\text{No. }& log \\
\hline 6800 & 3.8325 \\
\cos 77^{\circ} 12^{\prime} & \overline{1} .3455 \\
\hline 1507 & 3.1780
\end{array}$$
$$\begin{array}{r|l}
\text{No. }& \log \\
\hline 50 & 1.6990 \\
\sin 77^{\circ} 12^{\prime} & 1.9891 \\
\hline & 1.6881\\
74.95 & 1.8748 \\
\hline \sin 40^{\circ} 35^{\prime} & \overline{1} \cdot 8133
\end{array}$$
$\therefore$ Bearing of $P$ from $R$ is $\mathrm{S} 82^{\circ} 47^{\prime} \mathrm{E}$,
Let $x$ and $y$ be the two positive numbers such that $$ x+y=82 $$ Let product $P=x y$. $$ \begin{aligned} P &=x(82-x)=82 x-x^{2} \\ \frac{d P}{d x} &=82-2 x \end{aligned} $$ To find the largest value of $P, \frac{d P}{d x}=0$ $$ \begin{array}{r} 82-2 x=0 \\ 2 x=82 \\ x=41 \\ \frac{d^{2} P}{d x^{2}}=-2 \end{array} $$ When $x=41, \frac{d^{2} P}{d x^{2}}=-2 < 0$
$\therefore$ When $x=41$, the product is largest.
When $x=41, y=41$.
$\therefore$ The two positive numbers are 41 and 41 .
Click to Question Paper 2017 (D)
Solution 2
$$ \begin{gathered} f(x)=k x-1, g(x)=x+12 \\ (g \circ f)(2)=(f \circ g)(2) \\ g(f(2))=f(g(2)) \\ g(2 k-1)=f(14) \\ 2 k-1+12=14 k-1 \\ 12 k=12 \\ \therefore k=1 \end{gathered} $$
Click to Question Paper 2017 (D)
Solution 2 (OR)
Let $f(x)=x^{3}+p x^{2}-8 q x+5$ and $g(x)=2 x^{3}-q x^{2}+4 p x-18.$
Since $x-2$ is a common factor of $f(x)$ and $g(x)$, $$ \begin{aligned} \therefore f(2)=0 & \text { and } \quad g(2)=0 \\ 8+4 p-16 q+5 &=0 \\ 4 p-16 q &=-13 &\qquad (1)\\ g(2) &=0 \\ 16-4 q+8 p-18 &=0 \\ 8 p-4 q &=2 \\ 4 p-2 q &=1&\qquad (2) \end{aligned} $$ $$\begin{array}{rll} \text{Eq. (1)}\rightarrow 4 p-16 q&=-13&\cdots (3)\\ \text{Eq. (2)}\rightarrow 4 p-2 q&=1&\cdots (4)\\ (3)-(4):& -14 q=-14\end{array}$$ $\therefore q=1$, and Substitute $q=1$ in Eq. (2), $$ \begin{array}{r} 4 p-2=1 \\ 4 p=3 \\ \therefore p=\frac{3}{4} \\ \therefore p=\frac{3}{4}, q=1 \end{array} $$
Click to Question Paper 2017 (D)
Solution 3
\begin{aligned} &\quad \text { In an A.P., } \quad u_{p}=q, u_{q}=p \text {. }\\ &\begin{array}{r} u_{p}=q \\ a+(p-1) d=q&\cdots(1) \end{array}\\ & a+p d-d=q\\ & u_{q}=p\\ & a+(q-1) d=p\\ & a+q d-d=p&\cdots(2)\\ &\text { Eq. (1) } \rightarrow \quad a+p d-d=q&\cdots(3)\\ &\text { Eq. (2) } \rightarrow a+q d-d=p&\cdots(4)\\ &(3)-(4):(p-q) d=-(p-q)\\ &\therefore d=-1\\ & u_{p+q}=a+(p+q-1) d\\ &=a+p d+q d-d\\ &=a+p d-d+q d\\ &=q+q d\\ &=q+q(-1)\\ &\therefore u_{p+q}=0 \end{aligned}
Click to Question Paper 2017 (D)
Solution 3(OR)
$$\begin{array}{rr}\text { In a G.P, } & u_{1}-u_{2}=2 \\ & a-a r=2 \\ & a(1-r)=2 &\cdots (1)\\ & S=50\\ &\frac{a}{1-r}=50 & \cdots (2)\\ (1)\times (2):& a^2=100\\& a=\pm 10\end{array}$$ If $a=-10, 1-r=\frac{2}{-10}$. Thus $r=\frac 65$, which is impossible because $|r| < 1.$ Thus $a=10$.
Click to Question Paper 2017 (D)
Solution 4
Given: $O$ is the centre of the circle
To find: $\angle R Q T$
Click to Question Paper 2017 (D)
Solution 5
\begin{aligned} \sin 2 x(1+2 \cos x) &=\sin 2 x+2 \sin 2 x \cos x\\ &=\sin 2x+\left(\sin(2x+x)+\sin(2x-x)\right)\\ &=\sin 2x+\sin 3x+\sin x\\ &=\sin x+\sin 2 x+\sin 3 x \end{aligned}
Click to Question Paper 2017 (D)
Solution 6
\begin{aligned} &\lim _{x \rightarrow 2} \frac{x^{3}-8}{\sqrt{x+2}-2}\\ &=\lim _{x \rightarrow 2} \frac{(x-2)\left(x^{2}+2 x+4\right)}{\sqrt{x+2}-2} \times \frac{\sqrt{x+2}+2}{\sqrt{x+2}+2}\\ &=\lim _{x \rightarrow 2} \frac{(x-2)\left(x^{2}+2 x+4\right)(\sqrt{x+2}+2)}{x+2-4}\\ &=\lim _{x \rightarrow 2} \frac{(x-2)\left(x^{2}+2 x+4\right)(\sqrt{x+2}+2)}{x-2}\\ &=\lim _{x \rightarrow 2}\left[\left(x^{2}+2 x+4\right)(\sqrt{x+2}+2)\right]\\ &=\left(2^{2}+2(2)+4\right)(\sqrt{2+2}+2)\\ &=12 \times 4\\ &=48 \end{aligned} \begin{aligned} &\lim _{x \rightarrow 0} \frac{\cos x-1}{\sin ^{2} x} \\ =& \lim _{x \rightarrow 0} \frac{\cos x-1}{1-\cos ^{2} x} \\ =& \lim _{x \rightarrow 0} \frac{\cos x-1}{(1+\cos x)(1-\cos x)} \\ =& \lim _{x \rightarrow 0} \frac{-(1-\cos x)}{(1+\cos x)(1-\cos x)} \\ =& \lim _{x \rightarrow 0} \frac{-1}{1+\cos x} \\ =& \frac{-1}{1+\cos 0} \\ =& \frac{-1}{1+1} \\ =&-\frac{1}{2} \end{aligned}
Click to Question Paper 2017 (D)
Solution 7(a)
\begin{aligned} f(x) &=\frac{x}{x-3}, x \neq 3, g(x)=3 x+5 \\ (f\circ g)^{-1}(x)&=\frac 53\\ x& =(f\circ g)\left(\frac{5}{3} \right)\\ & =f \left(g\left(\frac{5}{3} \right)\right)\\ & =f \left(3\times \left(\frac{5}{3} \right)+5\right)\\ &=f(10)\\ & \therefore x=\frac{10}{10-3}=\frac{10}{7} \\ \end{aligned}
Solution 7(b)
$\odot$ is not a binary operation.
Click to Question Paper 2017 (D)
Solution 8(a)
Let $f(x)=x^{3}-a x-6$ $x+2$ is a factor of $f(x)$ $$ \begin{aligned} f(-2) &=0 \\ (-2)^{3}-a(-2)-6 &=0 \\ -8+2 a-6 &=0 \\ 2 a &=14 \\ \therefore a &=7 \end{aligned} $$ Let $g(x)=2 x^{3}+a x^{2}-6 x+9$
When $g(x)$ is divided by $x+1$, the remainder $=g(-1)$ $$ \begin{aligned} &=2(-1)^{3}+7(-1)^{2}-6(-1)+9 \\ &=-2+7+6+9 \\ &=20 \end{aligned} $$
Click to Question Paper 2017 (D)
Solution 8(b)
Solution 9(a)
$-7+(2 x+1)^{2} \geq 6 x$
$-7+4 x^{2}+4 x+1-6 x \geq 0$
$4 x^{2}-2 x-6 \geq 0$
$2 x^{2}-x-3 \geq 0$
$(x+1)(2 x-3) \geq 0$
$x+1 \leq 0$ and $2 x-3 \leq 0$ (or) $x+1 \geq 0$ and $2 x$
$x \leq-1$ and $x \leq \frac{3}{2}$ (or) $x \geq-1$ and $x \geq \frac{3}{2}$
$x \leq-1$ (or) $x \geq \frac{3}{2}$
The solution set $=\left\{x \mid x \leq-1\right.$ (or) $\left.x \geq \frac{3}{2}\right\}$
$\outsideeq{-1}{\frac 32}$
Click to Question Paper 2017 (D)
Solution 9(b)
$b, x, y, c$ are consecutive terms of a G.P. Let $r=$ common ratio. $$ \therefore x=b r, y=b r^{2}, c=b r^{3} $$ The A.M. between $b$ and $c$ is $a$. $$ \begin{aligned} \frac{b+c}{2} &=a \\ b+c &=2 a \\ x^{3}+y^{3} &=b^{3} r^{3}+b^{3} r^{6} \\ &=\left(b^{2}+b^{2} r^{3}\right) b r^{3} \\ &=\left(b+b r^{3}\right) b c \\ &=(b+c) b c \\ \therefore x^{3}+y^{3} &=2 a b c \end{aligned} $$
Click to Question Paper 2017 (D)
Solution 10(a)
In a G.P., $$\begin{array}{rll} u_{1} \times u_{2} \times u_{3}&=1000\\ a \times a r \times a r^{2}&=1000\\ a^{3} r^{3}&=1000\\ a r&=10&\cdots (1)\end{array}$$ $u_{1} ,u_{2}+6, u_{3}+7$ is an A.P.
$a, a r+6, a r^{2}+7$ is an A.P. $$\begin{array}{rll} a r+6-a&=a r^{2}+7-(a r+6)\\ 10+6-a&=10 r+7-16 \quad(\because a r=10)\\ 16-a &=10 r-9\\ a &=25-10 r\end{array}$$ Substitute $a=25-10 r$ in Eq. (1), $$ \begin{array}{r} (25-10 r) r=10 \\ 25 r-10 r^{2}-10=0 \\ 10 r^{2}-25 r+10=0 \\ 2 r^{2}-5 r+2=0 \\ (2 r-1)(r-2)=0 \\ r=\frac{1}{2}(\text { or }) r=2 \end{array} $$ When $r=\frac{1}{2}, a=20$
The first three terms of the GP. are $20,10,5$.
When $r=2, a=5$.
The first three terms of the G.P. are $5,10,20$
Click to Question Paper 2017 (D)
Solution 10(b)
$$ \begin{aligned} & A=\left(\begin{array}{cc} 4 & 1 \\ -9 & -2 \end{array}\right), B=\left(\begin{array}{cc} -3 & 1 \\ -1 & 2 \end{array}\right) \\ &\operatorname{det} A=-8-(-9)=1, A^{-1} \text { exists } \\ & A^{-1}=\frac{1}{\operatorname{det} A}\left(\begin{array}{cc} -2 & -1 \\ 9 & 4 \end{array}\right)=\frac{1}{1}\left(\begin{array}{cc} -2 & -1 \\ 9 & 4 \end{array}\right)=\left(\begin{array}{cc} -2 & -1 \\ 9 & 4 \end{array}\right) \\ & A^{2}=\left(\begin{array}{cc} 4 & 1 \\ -9 & -2 \end{array}\right)\left(\begin{array}{cc} 4 & 1 \\ -9 & -2 \end{array}\right)=\left(\begin{array}{cc} 16-9 & 4-2 \\ -36+18 & -9+4 \end{array}\right)=\left(\begin{array}{cc} 7 & 2 \\ -18 & -5 \end{array}\right) \\ & A X=2 B-A^{2}=\left(\begin{array}{cc} -6 & 2 \\ -2 & 4 \end{array}\right)-\left(\begin{array}{cc} 7 & 2 \\ -18 & -5 \end{array}\right)=\left(\begin{array}{cc} -13 & 0 \\ 16 & 9 \end{array}\right) \\ & A X=\left(\begin{array}{cc} -13 & 0 \\ 16 & 9 \end{array}\right) \\ & X=A^{-1}\left(\begin{array}{cc} -13 & 0 \\ 16 & 9 \end{array}\right)=\left(\begin{array}{cc} -2 & -1 \\ 9 & 4 \end{array}\right)\left(\begin{array}{cc} -13 & 0 \\ 16 & 9 \end{array}\right)=\left(\begin{array}{cc} 26-16 & -9 \\ -117+64 & 36 \end{array}\right) \\ &\therefore X=\left(\begin{array}{cc} 10 & -9 \\ -53 & 36 \end{array}\right) \end{aligned}$$
Click to Question Paper 2017 (D)
Solution 11(a)
\begin{aligned} &\text{Let } A=\left(\begin{array}{cc} 1 & 1 \\ -1 & 1 \end{array}\right)\\ &\det A=1-(-1)=2 \\ & A^{-1}=\frac{1}{\det A}\left(\begin{array}{ll} 1 & -1 \\ 1 & 1 \end{array}\right)=\frac{1}{2}\left(\begin{array}{ll} 1 & -1 \\ 1 & 1 \end{array}\right) \end{aligned} \begin{aligned} y-x&=1 \\ x+y&=3 \\ x+y&=3 \\ -x+y&=1 \\ \left(\begin{array}{ll} 1 & 1 \\ -1 & 1 \end{array}\right)\left(\begin{array}{l} x \\ y \end{array}\right)&=\left(\begin{array}{l} 3 \\ 1 \end{array}\right) \\ \left(\begin{array}{ll} x \\ y \end{array}\right)&=\left(\begin{array}{cc} 1 & 1 \\ -1 & 1 \end{array}\right)^{-1}\left(\begin{array}{l} 3 \\ 1 \end{array}\right)\\&=\frac{1}{2}\left(\begin{array}{ll} 1 & -1 \\ 1 & 1 \end{array}\right)\left(\begin{array}{l} 3 \\ 1 \end{array}\right)\\&=\frac{1}{2}\left(\begin{array}{l} 3-1 \\ 3+1 \end{array}\right)=\frac{1}{2}\left(\begin{array}{l} 2 \\ 4 \end{array}\right)=\left(\begin{array}{l} 1\\ 2 \end{array}\right)\\ \text{Thus }& x=1,y=2. \end{aligned}
Click to Question Paper 2017 (D)
Solution 11(b)
(i) only the first child is a boy
The set of favourable outccmes $=\{$ (B,G,G) $\}$
Number of favourable outcomes $=1$
$\therefore \mathrm{P}($ only the first child is a boy $)=\frac{1}{8}$
(ii) the last child is a boy
The set of favourable outcomes $=\{(\mathrm{B}, \mathrm{B}, \mathrm{B}),(\mathrm{B}, \mathrm{G}, \mathrm{B}),(\mathrm{G}, \mathrm{B}, \mathrm{B}),(\mathrm{G}, \mathrm{G}, \mathrm{B})\}$
Number of favourable outcomes $=4$
$\therefore \mathrm{P}($ the last child is a boy $)=\frac{4}{8}=\frac{1}{2}$
(iii) the last two children born are boys
The set of favourable outcomes $=\{(\mathrm{B}, \mathrm{B}, \mathrm{B}),(\mathrm{G}, \mathrm{B}, \mathrm{B})\}$
Number of favourable outcomes $=2$
$\therefore P($ the last two children born are boys $)=\frac{2}{8}=\frac{1}{4}$
Click to Question Paper 2017 (D)
Solution 12(a)
Prove: $A D$ bisects $\angle B A C$.
Proof: Draw a common tangent $P A Q$ at $A$. Join $D E$.
tangent to the smaller circle at $D$.
Proof: Draw a common tangent $P A Q$ at $A$. Join $D E$.
$\angle C D E=\alpha \quad($ Theorem 4$)$
$\angle P A B=\angle C \quad($ Theorem 4$)$
$\angle C D E+\angle C=\beta ($ Exterior $\angle$ of $\Delta C D E)$
$\angle P A D=\beta \quad($ Theorem 4$)$
$\therefore \angle P A B+\gamma=\angle C D E+\angle C$
$\angle C+\gamma=\alpha+\angle C$
$\therefore \quad \gamma=\alpha$
$\therefore A D$ bisects $\angle B A C .$
Click to Question Paper 2017 (D)
Solution 12(b)
Given : $P V$ is tangent and $Q T / / P V$.
Prove: $Q R S T$ is cyclic.
Proof: $\gamma=\beta$ (Theorem 4 )
$\begin{aligned} \alpha &=\beta \\ \therefore \alpha &=\gamma \end{aligned}$
$\alpha+\delta=180^{\circ}$
$\therefore \gamma +\delta=180^{\circ}$
$\therefore Q R S T$ is cyclic.
Click to Question Paper 2017 (D)
Solution 13(a)
Given : $\ln \triangle A B C, A D \perp B C, B E \perp A C, \angle A C D=45^{\circ}$
Prove: $\alpha(\triangle D E C): \alpha(\triangle A B C)=1: 2$
Proof: $\angle A D B=\angle A E B=90^{\circ}$
$\therefore A B D E$ is cyclic.
$\therefore \angle D E C=\angle A B C$
$\ln \triangle D E C$ and $\triangle A B C$ $$\begin{aligned} \angle D E C &=\angle A B C \quad \text { (proved) } \\ \angle C &=\angle C \\ \triangle D E C & \sim \triangle A B C \quad \text { (AA) } \end{aligned}$$ $$\begin{array}{rll} \frac{\alpha(\Delta D E C)}{\alpha(\Delta A B C)}&=\frac{D C^{2}}{A C^{2}}\\&=\left(\frac{D C}{A C}\right)^{2}\\&=\left(\cos 45^{\circ}\right)^{2}\\ &=\left(\frac{1}{\sqrt{2}}\right)^{2}=\frac{1}{2}\end{array}$$ $\therefore \alpha(\Delta D E C): \alpha(\Delta A B C)=1: 2$
Click to Question Paper 2017 (D)
Solution 13(b)
$P Q R S$ is a parallelogram. $$\begin{array}{rl} \vecAB{PQ}&=\vecAB{SR}\\ \vecAB{OQ}-\vecAB{OP}&=\vecAB{OR}-\vecAB{OS}\\ \left(\begin{array}{l}5 \\ 4\end{array}\right)-\left(\begin{array}{l}1 \\ 3\end{array}\right)&=\left(\begin{array}{l}1 \\ 9\end{array}\right)-\overrightarrow{O S}\\ \left(\begin{array}{l}4 \\ 1\end{array}\right)&=\left(\begin{array}{l}1 \\ 9\end{array}\right)-\overrightarrow{O S}\\ \overrightarrow{O S}&=\left(\begin{array}{l}1 \\ 9\end{array}\right)-\left(\begin{array}{l}4 \\ 1\end{array}\right)\\ \overrightarrow{O S}&=\left(\begin{array}{r}-3 \\ 8\end{array}\right) \end{array}$$ $\therefore$ The coordinates of $S$ is $(-3,8)$.
Click to Question Paper 2017 (D)
Solution 14(a)
$$\begin{array}{rcl} \frac{1+\tan ^{2} \alpha}{2-\sec ^{2} \alpha} &=&\frac{\sec ^{2} \alpha}{2-\sec ^{2} \alpha} \times \frac{\div \sec^2\alpha}{\div \sec^2\alpha}\\ &=&\frac{1}{\left(\frac{2}{\sec ^{2} \alpha} -1\right)}\\ &=&\frac{1}{2 \cos ^{2} \alpha-1} \\ &=&\frac{1}{\cos 2 \alpha} \\ &=&\sec 2 \alpha \end{array}$$
Click to Question Paper 2017 (D)
Solution 14(b)
Click to Question Paper 2017 (D)
Solution 15(a)
Solution 15(b)
Let $x$ and $y$ be the two positive numbers such that $$ x+y=82 $$ Let product $P=x y$. $$ \begin{aligned} P &=x(82-x)=82 x-x^{2} \\ \frac{d P}{d x} &=82-2 x \end{aligned} $$ To find the largest value of $P, \frac{d P}{d x}=0$ $$ \begin{array}{r} 82-2 x=0 \\ 2 x=82 \\ x=41 \\ \frac{d^{2} P}{d x^{2}}=-2 \end{array} $$ When $x=41, \frac{d^{2} P}{d x^{2}}=-2 < 0$
$\therefore$ When $x=41$, the product is largest.
When $x=41, y=41$.
$\therefore$ The two positive numbers are 41 and 41 .
Post a Comment