$\def\D{\displaystyle}$
1 (CIE 2012, s, paper 11, question 11either)
(i) Show that, for $\D x \ge 0, 9x^2 - x^3 \le 108.$ [4]
(ii) Find the area of the shaded region bounded by the curve, the line $\D AB$ and the y-axis. [6]
2 (CIE 2012, s, paper 11, question 11or)
(i) Find the coordinates of $\D P.$ [5]
(ii) Find the area of the shaded region bounded by the curve, the normal and the y-axis. [5]
3 (CIE 2012, s, paper 22, question 11either)
(i) Find the coordinates of $\D Q.$ [4]
(ii) Find the area of the shaded region bounded by the curve, the tangent and the x-axis. [7]
4 (CIE 2012, s, paper 22, question 11or)
(i) Given that $\D y = xe^{-x},$ find $\D \frac{dy}{dx}$ and hence show that $\D \int xe^{-x}dx=-xe^{-x}-e^{-x}+c.$ [4]
(ii) Find the area of the shaded region bounded by the curve, the tangent and the y-axis. [7]
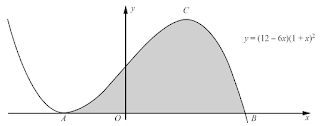
5 (CIE 2012, w, paper 11, question 12either)
(i) Find the coordinates of each of $\D A, B$ and $\D C.$ [6]
(ii) Find the area of the shaded region. [5]
6 (CIE 2012, w, paper 11, question 12or)
(i) the equation of the curve, [4]
(ii) the x-coordinate of $\D A$ and of $\D B,$ [3]
(iii) the area of the shaded region. [4]
7 (CIE 2012, w, paper 13, question 11either)
The tangent to the curve $\D y = 5e^x + 3e^{-x}$ at the point where $\D x = \ln\frac{3}{5},$ meets the x-axis at the point $\D P.$
(i) Find the coordinates of $\D P.$ [5]
The area of the region enclosed by the curve $\D y = 5e^x + 3e^{-x},$ the y-axis, the positive x-axis and
the line $\D x = a$ is 12 square units.
(ii) Show that $\D 5e^{2a} - 14e^a - 3 = 0.$ [3]
(iii) Hence find the value of $\D a.$ [3]
8 (CIE 2012, w, paper 22, question 12or)
(i) Find the coordinates of $\D Q.$ [4]
The line through $\D Q,$ parallel to the y-axis, meets the curve at $\D R$ and $\D OQRS$ is a rectangle.
(ii) Find $\D \int \left(8+e^{-\frac{x}{3}}\right)dx$ and hence find the area of the shaded region. [6]
9 (CIE 2013, w, paper 13, question 6)
Do not use a calculator in this question.
Show that the area of the shaded region can be written in the form $\D \frac{\sqrt{2}}{p},$ where $\D p$ is an integer to
be found. [6]
10 (CIE 2013, w, paper 21, question 11)
x-axis at $\D Q.$
(i) Find the coordinates of $\D Q.$ [4]
(ii) Find the area of the shaded region bounded by the curve, the coordinate axes and the tangent
to the curve at $\D P.$ [6]
11 (CIE 2014, s, paper 12, question 4)
The region enclosed by the curve $\D y = 2 \sin 3x,$ the x-axis and the line $\D x = a ,$ where
$\D 0<a<1$ radian, lies entirely above the x-axis. Given that the area of this region is $\D \frac{1}{3}$ square unit,
find the value of $\D a.$ [6]
12 (CIE 2014, s, paper 13, question 11)
(i) Find the x-coordinate of $\D A.$ [3]
(ii) Find $\D \frac{dy}{dx}$ and hence find the x-coordinate of $\D B.$ [4]
(iii) Showing all your working, find the area of the shaded region bounded by the curve, the x-axis
and the line through $\D B$ parallel to the y-axis. [5]
13 (CIE 2014, w, paper 13, question 11)
(i) Find the x-coordinates of the stationary points of the curve. [5]
(ii) Find $\D \int (x+5)(x-1)^2dx.$ [3]
(iii) Hence find the area enclosed by the curve and the x-axis. [2]
(iv) Find the set of positive values of $\D k$ for which the equation $\D (x+5)(x-1)^2=k$ has only one real solution. [2]
14 (CIE 2014, w, paper 21, question 12)
(i) Show that $\D x-2$ is a factor of $\D 3x^3-14^2+32.$
(ii) Hence factorise $\D 3x^3-14x^2+32$ completely.
(iii) State the x-coordinates of $\D P$ and $\D Q.$ [1]
(iv) Find $\D \int (3x-14+\frac{32}{x^2})dx$ and hence determine the area of the shaded region. [4]
15 (CIE $2015, \mathrm{~s}$, paper 11, question 9)
The diagram shows parts of the line $y=3 x+10$ and the curve $y=x^{3}-5 x^{2}+3 x+10$. The line and the curve both pass through the point $A$ on the $y$ -axis. The curve has a maximum at the point $B$ and a minimum at the point $C$. The line through $C$, parallel to the $y$ -axis, intersects the line $y=3 x+10 \quad$ at the point $D$.
(i) Show that the line $A D$ is a tangent to the curve at $A$. $[2]$
(ii) Find the $x$ -coordinate of $B$ and of $C$. [3]
(iii) Find the area of the shaded region $A B C D$, showing all your working. $[5]$
16 (CIE $2015, \mathrm{~s}$, paper 22, question 8)
The graph of $y=x^{2}-6 x+10$ cuts the $y$ -axis at $A$. The graphs of $y=x^{2}-6 x+10$ and $y=x+10$ cut one another at $A$ and $B$. The line $B C$ is perpendicular to the $x$ -axis. Calculate the area of the shaded region enclosed by the curve and the line $A B$, showing all your working. $\quad[8]$
17 (CIE $2015, \mathrm{w}$, paper 11, question 9)
You are not allowed to use a calculator in this question.
(i) Find $\int \sqrt{4+x} \mathrm{~d} x$. $[2]$
(ii) The diagram shows the graph of $y=\sqrt{4+x}$, which meets the $y$ -axis at the point $A$ and the line $x=5$ at the point $B$. Using your answer to part (i), find the area of the region enclosed by the curve and the straight line $A B$.
18 (CIE 2016, s, paper 12, question 7)
The diagram shows part of the graph of $y=1-2 \cos 3 x$, which crosses the $x$ -axis at the point $A$ and has a maximum at the point $B$.
(i) Find the coordinates of $A$.
(ii) Find the coordinates of $B$.[2]
(iii) Showing all your working, find the area of the shaded region bounded by the curve, the $x$ -axis and the perpendicular from $B$ to the $x$ -axis.
19 (CIE 2016, s, paper 21, question 11 )
(i) Find $\int\left(3 x-x^{ \frac{3}{2}}\right) \mathrm{d} x .$
The diagram shows part of the curve $y=3 x-x^{\frac{3}{2}}$ and the lines $y=3 x$ and $2 y=27-3 x$. The curve and the line $y=3 x$ meet the $x$ -axis at $O$ and the curve and the line $2 y=27-3 x$ meet the $x$ -axis at $A$.
(ii) Find the coordinates of $A$.
(iii) Verify that the coordinates of $B$ are $(3,9)$. [1]
(iv) Find the area of the shaded region. $[4]$
20 (CIE 2016, w, paper 11, question 7)
The diagram shows part of the graph of $y=2 \cos \left(x-\frac{\pi}{6}\right)$. The graph intersects the $y$ -axis at the point $A$, has a maximum point at $B$ and intersects the $x$ -axis at the point $C$.
(i) Find the coordinates of $A$. $[1]$
(ii) Find the coordinates of $B$. $[2]$
(iii) Find the coordinates of $C$. $[2]$
(iv) Find $\int 2 \cos \left(x-\frac{\pi}{6}\right) \mathrm{d} x$. $[1]$
(v) Hence find the area of the shaded region. $[2]$
21 (CIE 2017 , march, paper 12, question 10)
The diagram shows part of the curve $y=(2 x-5)^{\frac{3}{2}}$ and the line $y=3 \sqrt{3}$. The curve meets the $x$ -axis at the point $A$ and the line $y=3 \sqrt{3}$ at the point $B$. Find the area of the shaded region enclosed by the line $A B$ and the curve, giving your answer in the form $\frac{p \sqrt{3}}{20}$, where $p$ is an integer. You must show all your working. $[8]$
22 (CIE 2017, s, paper 22, question 11)
The diagram shows part of the curve $y=x^{3}+4 x^{2}-5 x+5$ and the line $y=5$. The curve and the line intersect at the points $A, B$ and $C .$ The points $D$ and $E$ are on the $x$ -axis and the lines $A E$ and $C D$ are parallel to the $y$ -axis.
(i) Find $\int\left(x^{3}+4 x^{2}-5 x+5\right) \mathrm{d} x$. $[2]$
(ii) Find the area of each of the rectangles $O E A B$ and $O B C D$. $[4]$
(iii) Hence calculate the total area of the shaded regions enclosed between the line and the curve. You must show all your working. $[4]$
23 (CIE 2017, s, paper 23, question 11)
The diagram shows part of the curve $y=5+\sqrt{10 x}$ and the line $4 y=5 x+20 .$ The line and curve intersect at the points $P(0,5)$ and $Q .$ The line $Q R$ is parallel to the $y$ -axis.
(i) Find the coordinates of $Q$. $[4]$
(ii) Find the area of the shaded region. You must show all your working. $[6]$
24 (CIE $2017, \mathrm{w}$, paper 11, question 5$)$
The diagram shows part of the graph of $y=4 \mathrm{e}^{2 x}+16 \mathrm{e}^{-2 x}$ meeting the $y$ -axis at the point $A$ and the line $x=1$ at the point $B$.
(i) Find the coordinates of $A$. $[1]$
(ii) Find the $y$ -coordinate of $B$. $[1]$
(iii) Find $\int\left(4 \mathrm{e}^{2 x}+16 \mathrm{e}^{-2 x}\right) \mathrm{d} x$ $[2]$
(iv) Hence find the area of the shaded region enclosed by the curve and the line $A B$. You must show all your working.
25 (CIE $2017, \mathrm{w}$, paper 22, question 11$)$
The diagram shows the curve $y=4+3 x-x^{2}$ intersecting the positive $x$ -axis at the point $A$. The line $y=m x+8 \quad$ is a tangent to the curve at the point $B$. Find
(i) the coordinates of $A$, $[2]$
(ii) the value of $m$, $[3]$
(iii) the coordinates of $B$, [2]
(iv) the area of the shaded region, showing all your working. $[5]$
Answers
1. (ii) $\D 628$
2. (i) $\D (0, 1.58)$
(ii) $\D 0.292$
3. (i) $\D x = 2 + \frac{3\pi}{2}$
(ii) $\D \frac{3\sqrt{2}}{2}-2$
4. $\D (9/e^2) - 1$
5. (i) $\D A(-1, 0),B(2, 0),
C(1, 24)$
(ii) $\D 40.5$
6. (i) $\D y = x^3 - 3x^2 - 9x + 30$
(ii) $\D x = -1, 3$
(iii) $\D 76$
7. (i) $\D P(3.49, 0)$
(ii)
(iii) $\D \ln 3$
8. (i) $\D Q(-3, 0)$
(ii) $\D 8x - 3e^{-\frac{x}{3}}, A = 3$
9. $\D \frac{\sqrt{2}}{3}$
10. (i) $\D (6, 0)$
(ii) $\D 27.1$
11. $\D a =\frac{\pi}{9}$
12. (i) $\D x = \frac{5\pi}{18}$
(ii) $\D \frac{dy}{dx} = 3\sqrt{3} \cos 3x - 3 \sin 3x$
(iii) $\D A = \frac{2}{3}$
13. (i) $\D x = 1,-3$
(ii) $\D \frac{x^4}{4}+x^3- \frac{9x^2}{2}+5x.$
(iii) $\D 108$ (iv) $\D k > 32$
14. (ii) $\D (x - 2)(x - 4)(3x + 4)$
(iii) $\D x = 2, 4,$
(iv) $\D 2$
15. (ii) $x=1 / 3,3(\mathrm{iii}) 99 / 4$
16. $343 / 6$
17. (i) $2(4+x)^{3 / 2} / 3$
(ii) $A=1 / 6$
18. (i) $x=\pi / 9$
(ii) $(\pi / 3,3)(\mathrm{iii}) 1.28$
19. (i) $3 x^{2} / 2-2 x^{5 / 2} / 5$
(ii) $(9,0)$, (iv) $16.2$
20. (i) $(0, \sqrt{3})(\mathrm{ii})(\pi / 6,2)$
(iii) $2 \pi / 3($ iv $) 2 \sin (x-\pi / 6)$
(v)3
21. $9 \sqrt{3} / 20$
22. (i) $x^{4} / 4+4 x^{3} / 3-5 x^{2} / 2+5 x$
(ii) 25,5
(iii) $886 / 12$
23. (i) $x=6.4, y=13$
(ii) $8.53$
24. (i) $(0,20)$,
(ii) 31,7
(iii) $2 e^{2 x}-8 e^{-2 x}(+c)$
(iv) $6.16$
25. $(4,0),-1,(2,6), 32 / 3$
Post a Comment